早教吧作业答案频道 -->数学-->
如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.(1)求证:△ABF≌△CBE;(2)判断△CEF的形状,并说明理由.
题目详情
如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
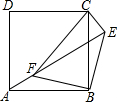
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有
,
∴△ABF≌△CBE(SAS).
(2) △CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°-∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB-∠FEB=135°-45°=90°,
∴△CEF是直角三角形.
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有
|
∴△ABF≌△CBE(SAS).
(2) △CEF是直角三角形.理由如下:

∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°-∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB-∠FEB=135°-45°=90°,
∴△CEF是直角三角形.
看了 如图,点E正方形ABCD外一...的网友还看了以下:
在三相交流电路中,负载为星形连接,A相为电阻,B相为电感,C相为电容,通过这三相负载的电流的有效值 2020-05-17 …
正方形ABCD的边长为2,点E在边AD上移动,连接BE,作AP垂直于BE于P,连接CP,点Q在AB 2020-05-17 …
已知△BCE、△DCF分别是以平行四边形ABCD的邻边BC、CD为边向外所作的等边三角形求证:△A 2020-05-17 …
(4分)电流-电压两用电表的电路如图(a)所示.已知图中S是双刀双掷电键,其外形见图(b),a、b 2020-07-07 …
一个三角形ABC,角A为60度,角B角C的角平分线分别交AB于D交AC于E两线交于点F连接D,E有 2020-07-30 …
已知正方形ABCD中,边长为4,E为AB边上的一动点,(E与A,B点不重合),设AE=x,以E为顶 2020-08-03 …
已知正方形ABCD中,边长为4,E为AB边上的一动点,(E为A,B点不重合),设AE=x,以E为顶 2020-08-03 …
已知正方形ABCD中,边长为4,E为AB边上的一动点,(E与A,B点不重合),设AE=x,以E为顶 2020-08-03 …
已知正方形ABCD中,边长为4,E为AB边上的一动点,(E与A,B点不重合),设AE=x,以E为顶 2020-08-03 …
(2005•常州)如图所示,为使滑动变阻器的滑片P向右移动时,通电螺线管对条形磁铁的斥力变大,则电源 2020-11-12 …