早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.(1)求OE的长及经过O,D,C三点
题目详情
如图,在矩形ABCD中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
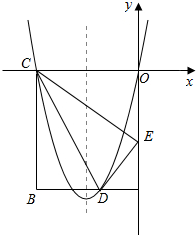
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.

(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(1)∵CE=CB=5,CO=AB=4,
∴在Rt△COE中,OE=3,
设AD=m,则DE=BD=4-m,
∵OE=3,
∴AE=5-3=2,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,即m2+22=(4-m)2,解得m=
,
∴D(-
,-5),
∵C(-4,0),O(0,0),
∴设过O、D、C三点的抛物线为y=ax(x+4),
∴-5=-
a(-
+4),解得a=
,
∴抛物线解析式为y=
x(x+4)=
x2+
x;
(2)∵CP=2t,
∴BP=5-2t,
在Rt△DBP和Rt△DEQ中,
,
∴Rt△DBP≌Rt△DEQ(HL),
∴BP=EQ,
∴5-2t=t,
∴t=
;
(3)∵抛物线的对称为直线x=-2,
∴设N(-2,n),
又由题意可知C(-4,0),E(0,-3),
设M(m,y),
①当EN为对角线,即四边形ECNM是平行四边形时,
则线段EN的中点横坐标为
=-1,线段CM中点横坐标为
,
∵EN,CM互相平分,
∴
=-1,解得m=2,
又M点在抛物线上,
∴y=
×22+
×2=16,
∴M(2,16);
②当EM为对角线,即四边形ECMN是平行四边形时,
则线段EM的中点横坐标为
,线段CN中点横坐标为
=-3,
∵EN,CM互相平分,
∴
=-3,解得m=-6,
又∵M点在抛物线上,
∴y=
×(-6)2+
×(-6)=16,
∴M(-6,16);
③当CE为对角线,即四边形EMCN是平行四边形时,
则M为抛物线的顶点,即M(-2,-
).
综上可知,存在满足条件的点M,其坐标为(2,16)或(-6,16)或(-2,-
).
∴在Rt△COE中,OE=3,
设AD=m,则DE=BD=4-m,
∵OE=3,
∴AE=5-3=2,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,即m2+22=(4-m)2,解得m=
| 3 |
| 2 |
∴D(-
| 3 |
| 2 |
∵C(-4,0),O(0,0),
∴设过O、D、C三点的抛物线为y=ax(x+4),
∴-5=-
| 3 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
∴抛物线解析式为y=
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
(2)∵CP=2t,
∴BP=5-2t,
在Rt△DBP和Rt△DEQ中,
|
∴Rt△DBP≌Rt△DEQ(HL),
∴BP=EQ,
∴5-2t=t,
∴t=
| 5 |
| 3 |
(3)∵抛物线的对称为直线x=-2,
∴设N(-2,n),
又由题意可知C(-4,0),E(0,-3),
设M(m,y),
①当EN为对角线,即四边形ECNM是平行四边形时,
则线段EN的中点横坐标为
| 0+(-2) |
| 2 |
| m-4 |
| 2 |
∵EN,CM互相平分,
∴
| m-4 |
| 2 |
又M点在抛物线上,
∴y=
| 4 |
| 3 |
| 16 |
| 3 |
∴M(2,16);
②当EM为对角线,即四边形ECMN是平行四边形时,
则线段EM的中点横坐标为
| m+0 |
| 2 |
| -2-4 |
| 2 |
∵EN,CM互相平分,
∴
| m |
| 2 |
又∵M点在抛物线上,
∴y=
| 4 |
| 3 |
| 16 |
| 3 |
∴M(-6,16);
③当CE为对角线,即四边形EMCN是平行四边形时,
则M为抛物线的顶点,即M(-2,-
| 16 |
| 3 |
综上可知,存在满足条件的点M,其坐标为(2,16)或(-6,16)或(-2,-
| 16 |
| 3 |
看了 如图,在矩形ABCD中,OA...的网友还看了以下:
如图,矩形ABCD中,E是AD上的一点,过 点E作EF⊥EC交边AB于点F,EF=EC,若矩形AB 2020-05-16 …
已知梯形ABCD,AB平行BC,AB=AD=5,tan角DBC=3、4,E为射线BD上一动点,过点 2020-05-16 …
正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标 2020-05-16 …
过四边形ABCD的对角线交点O画CD的平行线,分别与边BC,AD及AB的延长线交与E,F,G,求证 2020-05-17 …
如图,抛物线y=-1/2x²+5/2x-2与X轴相交于A,B,与y轴相交于点C,过点C作CD∥X轴 2020-06-06 …
在等边三角形ABC中,AB=8,点D在边BC上,三角形ADE为等边三角形,且点E与点D在直线AC的 2020-06-12 …
四边形ABCD为正方形,点E为射线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以D 2020-06-18 …
如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接 2020-07-10 …
复合函数求导问题复合函数求导时,遇到一种函数通过不同形式两两组合可得到不同的结果时,应该如何解决例如 2020-12-13 …
正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴上,且A的坐标是(1,0) 2020-12-25 …