早教吧作业答案频道 -->数学-->
如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想:(1)△BCG与△ACH全等吗?若全等,请说明理由.(2)M、N分别是BE、AD的中点.①△BCM≌△CAN吗
题目详情
如图,△ABC和△CDE是两个不全等的等边三角形.AC、AD分别交BE与G、F点,AD与CE交于H点.猜想:
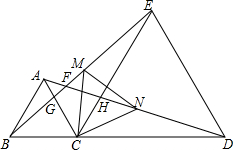
(1)△BCG与△ACH全等吗?若全等,请说明理由.
(2)M、N分别是BE、AD的中点.
①△BCM≌△CAN吗?
②△CMN是等边三角形吗?

(1)△BCG与△ACH全等吗?若全等,请说明理由.
(2)M、N分别是BE、AD的中点.
①△BCM≌△CAN吗?
②△CMN是等边三角形吗?
▼优质解答
答案和解析
(1)△BCG与△ACH全等,
∵△ABC、△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACB+∠BCD=∠ACD,
∠DCE+∠BCD=∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠EBC,
∵∠ACB=∠DCE=60°,
∴∠ACH=180°-∠ACB-∠DCE=60°,
∴∠ACB=∠ACH,
在△BCG和△ACH中,
,
∴△BCG≌△ACH.
(2)①△BCM≌△CAN,
∵△ACD≌△BCE,
∴∠EBC=∠CAD,BE=AD,
∵M、N分别是BE、AD的中点,
∴BM=AN,
在△BCM和△CAN中,
,
∴△BCM≌△CAN(SAS).
②△MNC是等边三角形.
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵点M、N分别是线段AD、BE的中点,AD=BE,
∴AM=BN,
在△ACM和△BCN中,
,
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
∴∠MCN=∠BCM+∠BCN=∠BCM+∠ACM=∠ACB=60°,
∴△MNC是等边三角形.
∵△ABC、△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACB+∠BCD=∠ACD,
∠DCE+∠BCD=∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴∠CAD=∠EBC,
∵∠ACB=∠DCE=60°,
∴∠ACH=180°-∠ACB-∠DCE=60°,
∴∠ACB=∠ACH,
在△BCG和△ACH中,
|
∴△BCG≌△ACH.
(2)①△BCM≌△CAN,
∵△ACD≌△BCE,
∴∠EBC=∠CAD,BE=AD,
∵M、N分别是BE、AD的中点,
∴BM=AN,
在△BCM和△CAN中,
|
∴△BCM≌△CAN(SAS).
②△MNC是等边三角形.
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵点M、N分别是线段AD、BE的中点,AD=BE,
∴AM=BN,
在△ACM和△BCN中,
|
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
∴∠MCN=∠BCM+∠BCN=∠BCM+∠ACM=∠ACB=60°,
∴△MNC是等边三角形.
看了 如图,△ABC和△CDE是两...的网友还看了以下:
等边三角形ABC在平面直角坐标系中,点B,A分别在X轴的正负半轴上,点O恰好在AB的中点上,点C在 2020-05-16 …
已知点A(2a—b,a+3b)到y轴的距离和到原点的距离都是7,求点B(a²-b ,b²-a)到x 2020-05-16 …
一道高中不等式的证明题a>b>0,如何证明2a+b/a+2b>a/b不总成立?(正证、反证皆可)原 2020-06-06 …
椭圆求证问题已知椭圆x²/a²+y²/b²=1短轴的两端点为点A、点B.(a>b>0)P为椭圆上不 2020-07-07 …
有关转置矩阵,迷惑中.把一个m×n矩阵的行,列互换得到的n×m矩阵,称为A的转置矩阵,记为A'如何 2020-07-25 …
在平面直角坐标系中,已知点a(a+b.2-a)与点b(a-5.b-2a)关于y轴对称.(1)试确点 2020-07-30 …
辅助角公式对于acosx+bsinx型函数,我们可以如此变形acosx+bsinx=√(a²+b² 2020-08-02 …
中心对称图形问题如图,L1垂直L2垂足是点O点A与点B关于直线L1轴对称,点A与点C关于点O中心对 2020-08-03 …
已知直线AC:y=-根号3/3x+2/3根号3交两坐标于A,C,△OAB是等腰直角三角形,∠B=90 2020-12-31 …
已知如图,直线AB:y=-x+8与x轴,y轴分别交与点B,A,过点B作直线AB的垂线交y轴与点D已知 2021-01-11 …