如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（）A.当P为BC中点，△APD是等边三角形B.当△ADE∽△BPE时，P为BC中点C.

Question

如图，在矩形ABCD中，P是BC上一点，E是AB上一点，PD平分∠APC，PE⊥PD，连接DE交AP于F，在以下判断中，不正确的是（　　）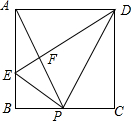

A. 当P为BC中点，△APD是等边三角形

B. 当△ADE∽△BPE时，P为BC中点

C. 当AE=2BE时，AP⊥DE

D. 当△APD是等边三角形时，BE+CD=DE

Answer 1

A、∵四边形ABCD是矩形，
∴AB=CD，∠A=∠B，
∵点P是BC的中点，
∴PB=PC，
在△APB和△DPC中，

AB=DC

∠ABP=∠DCP

PB=PC

，
∴△APB≌△DPC，
∴PA=PD，∠APB=∠DPC，
∵PD平分∠APC，
∴∠APD=∠CPD，
∴∠APB=∠APD=∠CPD，
∵∠APB+∠APD+∠CPD=180°，
∴∠APD=60°，
∵PA=PD，
∴△APD是等边三角形；
∴A正确，故A不符合题意；

C、∵PD⊥PE，
∴∠BPE+∠DPC=90°，∠APE+∠APD=90°，
∵∠APD=∠CPD，
∴∠APE=∠BPE，
∴(BP)/(AP)=(BE)/(AE)，
∵AE=2BE，
∴(BP)/(AP)=(1)/(2)，
在Rt△ABP中，sin∠BAP=(BP)/(AP)=(1)/(2)，
∴∠BAP=30°，
∴∠APB=60°，
∴∠BPE=∠APE=30°=∠BAP，
∴AE=PE，
∵EA⊥AD，EP⊥PD，
∴∠ADE=∠PDE，
在△ADE和△PDE中，

∠ADE=∠PDE

∠DAE=∠DPE

AE=PE

，
∴△ADE≌△PDE，
∴∠AED=∠PED，
∵AE=PE，
∴DE⊥AP，
∴C正确，故C不符合题意；

D、∵△APD是等边三角形，
∴AP=DP，∠APD=60°，
∴∠CPD=60°，
∴∠APB=60°，
∴∠BPE=∠APE=∠PAB=30°
∴AE=PE
设BE=a，
在Rt△PBE中，BP=√(3)BE=√(3)a，PE=2a，
∴AE=2a，
∴CD=AB=BE+AE=3a，
易证△APB≌△DPC，
∴PB=PC，
∴AD=BC=2BP=2√(3)a，
在Rt△ADE中，根据勾股定理，得，DE=√(AE2+AD2)=4a，
∵BE+CD=a+3a=4a=DE，
∴D正确，故D不符合题意；
∴符合题意的只有B．
故选B．