早教吧作业答案频道 -->数学-->
用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.甲同学说:“当正方形的一边在最长边时,剪出的内接正方形最大”;乙同学说:“当正方形的一边在最短边上
题目详情
用一个大小形状固定的不等边锐角三角形纸,剪出一个最大的正方形纸备用.
甲同学说:“当正方形的一边在最长边时,剪出的内接正方形最大”;
乙同学说:“当正方形的一边在最短边上时,剪出的内接正方形最大”;
丙同学说:“不确定,剪不出这样的正方形纸.”
你认为谁说的有道理,请证明.
(假设图中△ABC的三边a,b,c,且a>b>c,三边上的高分别记为ha,hb,hc)
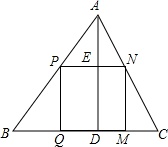
甲同学说:“当正方形的一边在最长边时,剪出的内接正方形最大”;
乙同学说:“当正方形的一边在最短边上时,剪出的内接正方形最大”;
丙同学说:“不确定,剪不出这样的正方形纸.”
你认为谁说的有道理,请证明.
(假设图中△ABC的三边a,b,c,且a>b>c,三边上的高分别记为ha,hb,hc)

▼优质解答
答案和解析
设△ABC的三条边上的对应高分别为ha,hb,hc.
由(1)、(2)可得:
=
,
∴xa=
,
同理xb=
,xc=
,
∵xa-xb=
-
=
-
b+hb=2S(
-
),
=
(b+hb-a-ha),
=
(b-a)(1-
),
∵a>b,ha<b,
∴(b-a)(1-
)<0,
即xa-xb<0,
∴xa<xb,
同理:xb<xc,
∴xa<xb<xc.
∴乙同学说的正确.
由(1)、(2)可得:
| xa |
| a |
| ha-xa |
| ha |
∴xa=
| aha |
| a+ha |
同理xb=
| bhb |
| b+hb |
| chc |
| c+hc |
∵xa-xb=
| aha |
| a+ha |
| bhb |
| b+hb |
| 2s |
| a+ha |
| 2s |
| 1 |
| a+ha |
| 1 |
| b+hb |
=
| 2s |
| (a+ha)(b+hb) |
=
| 2s |
| (a+ha)(b+hb) |
| ha |
| b |
∵a>b,ha<b,
∴(b-a)(1-
| ha |
| b |
即xa-xb<0,
∴xa<xb,
同理:xb<xc,
∴xa<xb<xc.
∴乙同学说的正确.
看了 用一个大小形状固定的不等边锐...的网友还看了以下:
把两个小的正方形剪开怎样能合成一个大的正方形 2020-05-13 …
要把由5个小正方形组成的十字形纸板剪开,使剪成的若干块能够拼成一个大的正方形(1)如果剪4刀,应如 2020-05-13 …
把一个长为2a,宽为2b的长方形沿虚线剪开分成四个大小相等的长方形(图①),然后如图②所示拼成一个 2020-05-13 …
把棱长分别为2.15cm和3.24cm的两个正方体铁块熔化,制成一个大的正方体铁块,求这个大正方体 2020-05-14 …
如何把五个同样大小的正方形剪接成一个大的正方形? 2020-05-17 …
数学活动:拼图中的数学数学活动课上,老师提出如下问题:用5个边长为1的小正方形组合一个图形(相互之 2020-05-17 …
正方体的应用8个棱长为2厘米的小正方体拼成的一个大正方体.问这个大正方体的表面积是多少?如果任意拿 2020-05-21 …
把若干个体积相同的小正方体堆成一个大的正方体,然后在大正方体的表面涂上颜色,已知两面被涂上红色的小 2020-05-23 …
512个小正方体组成一个大的正方体,然后把这个大正方体表面涂上红色,再把这个大正方体分成原来的51 2020-08-01 …
一个大的正方形,在里面画一个最大的圆,圆中再画一个最大的正方形,求这个正方形占大正方形的几分之几?怎 2020-12-25 …