早教吧作业答案频道 -->数学-->
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)若CE=12,CF=5,求OC的长;(2)当点O在边AC上运动时,四边形BCFE会是菱形
题目详情
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
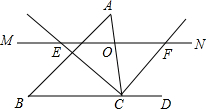
(1)若CE=12,CF=5,求OC的长;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.

(1)若CE=12,CF=5,求OC的长;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
▼优质解答
答案和解析
(1) 如图1中,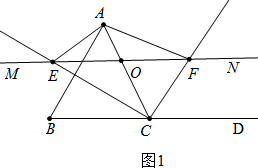 ∵CE平分∠BCA,CF平分∠ACD,
∵CE平分∠BCA,CF平分∠ACD,
∴∠ACE=∠ECB=
∠ACB,∠ACF=∠FCD=
∠ACD,
∴∠ACE+∠ACF=
(∠ACB+∠ACD)=90°,
∴∠ECF=90°,
∵MN∥BC,
∴∠OEC=∠ECB=∠OCE,∠OFC=∠FCD=∠FCO,
∴EO=OC=FO,
在RT△ECF中,∵∠ECF=90°,EC=12,CF=5,
∴EF=
=
=13,
∴OC=
EF=
.
(2)如图2中,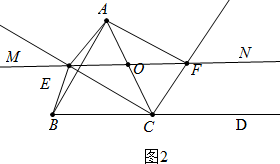 四边形BCFE不可能是菱形.
四边形BCFE不可能是菱形.
由(1)可知∠ECF=90°,
∴EF>CF,
∴四边形BCFE不可能是菱形.
(3)如图3中,当点O运动到AC等中点,且∠ACB=90°时四边形AECF是正方形.
证明:由(1)可知OC=OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵AC=EF,
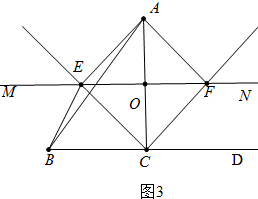 ∴四边形AECF是矩形,
∴四边形AECF是矩形,
∵MN∥BC,
∵∠AOE=∠ACB=90°,
∴EO⊥AC,∵OA=OC,
∴EA=EC,
∴四边形AECF是正方形.
 ∵CE平分∠BCA,CF平分∠ACD,
∵CE平分∠BCA,CF平分∠ACD,∴∠ACE=∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ACE+∠ACF=
| 1 |
| 2 |
∴∠ECF=90°,
∵MN∥BC,
∴∠OEC=∠ECB=∠OCE,∠OFC=∠FCD=∠FCO,
∴EO=OC=FO,
在RT△ECF中,∵∠ECF=90°,EC=12,CF=5,
∴EF=
| EC2+CF2 |
| 122+52 |
∴OC=
| 1 |
| 2 |
| 13 |
| 2 |
(2)如图2中,
 四边形BCFE不可能是菱形.
四边形BCFE不可能是菱形.由(1)可知∠ECF=90°,
∴EF>CF,
∴四边形BCFE不可能是菱形.
(3)如图3中,当点O运动到AC等中点,且∠ACB=90°时四边形AECF是正方形.
证明:由(1)可知OC=OE=OF,
∵OA=OC,OE=OF,
∴四边形AECF是平行四边形,
∵AC=EF,
 ∴四边形AECF是矩形,
∴四边形AECF是矩形,∵MN∥BC,
∵∠AOE=∠ACB=90°,
∴EO⊥AC,∵OA=OC,
∴EA=EC,
∴四边形AECF是正方形.
看了 如图,△ABC中,点O是边A...的网友还看了以下:
平面直角坐标系中四边形的存在性问题在平面直角坐标中,有点O(0,0),A(-1,1),B(2,2)( 2020-03-31 …
读“经纬网图”,完成下列要求.(1)写出图中A、B、C、D四点的经纬度:A.;B.;C.;D..( 2020-05-02 …
1.设a.b.c分别是三角形ABC的三条边,且a/b=a+1/a+b+c,是判断∠A,∠B的关系. 2020-05-13 …
A.B.C.D四个人谁是小偷的问题A、B、C、D这四个人当中有个是小偷.他们四个是一个寝室的,一天 2020-05-17 …
简单逻辑题已知A,B,C,D四个人中有一个人是小偷。并且,这四个人中每人要么说真话要么说假话。在审 2020-07-08 …
用反证法证明真命题“四边形中至少有一个角是钝角或直角”时,应假设()A.四边形中至多有一个角是钝角 2020-08-01 …
(八年级人教版数学暑期作业)已知在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,其中a=5,c 2020-11-01 …
(2014•孝感二模)如图所示,真空空间中四点O、A、B、C恰为一棱长为L的正四面体的四个顶点,其中 2020-11-12 …
有A,B,C,D四位客人,应分别入住a,b,c,d四间客房,现在这四人各自随意入住这四间客房中的一间 2020-12-10 …
A,B,C,D四种常见元素,已知A元素的原子中不含中子.A,B,C,D四种常见元素,已知A元素的原子 2021-02-01 …