早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB中点,DE交AB于点G求证:(1)DF=AC;(2)GD=GE.
题目详情
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABD和△ACE都是等边三角形,F为AB中点,DE交AB于点G
求证:(1)DF=AC;(2)GD=GE.
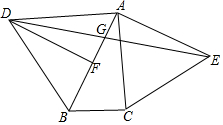
求证:(1)DF=AC;(2)GD=GE.

▼优质解答
答案和解析
证明:(1)∵∠ACB=90°,∠BAC=30°,
∴BC=
AB,∠ABC=60°,
∵F为AB中点,
∴BF=
AB,
∴BF=BC,
又∵△ABD是等边三角形,
∴BD=AB,∠ABD=60°,
在△DBF和△ABC中,
∵
,
∴△DBF≌△ABC,
∴DF=AC;
(2)∵△ACE为等边三角形,
∴AC=AE,∠CAE=60°,
又∵DF=AC,∠BAC=30°,
∴DF=EA,∠GAE=90°,
∵△ABD为等边三角形,且F为AB中点,
∴DF⊥AB,即∠DFG=90°,
在△DFG和△EAG中,
∵
,
∴△DFG≌△EAG(AAS),
∴DG=EG.
∴BC=
| 1 |
| 2 |
∵F为AB中点,
∴BF=
| 1 |
| 2 |
∴BF=BC,
又∵△ABD是等边三角形,
∴BD=AB,∠ABD=60°,
在△DBF和△ABC中,
∵
|
∴△DBF≌△ABC,
∴DF=AC;
(2)∵△ACE为等边三角形,
∴AC=AE,∠CAE=60°,
又∵DF=AC,∠BAC=30°,
∴DF=EA,∠GAE=90°,
∵△ABD为等边三角形,且F为AB中点,
∴DF⊥AB,即∠DFG=90°,
在△DFG和△EAG中,
∵
|
∴△DFG≌△EAG(AAS),
∴DG=EG.
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
在一定温度下,化学平衡常数K=(C)c(D)d / (A)a(B)b.给定AB的浓度 达到平衡 就 2020-04-06 …
24 (a+b)/(c+d)=(√a^2+b^2)/√ (c^2+d^2)成立证明:(1)a/b= 2020-05-14 …
关于比例的基本性质已知a比b等于c比d(b+或-d不等于0),求证:a+c比a-c等于b+d比b- 2020-05-16 …
现有A,B,C,D四种物质,已知A,B为黑色粉末,C,D为无色气体,A,B在高温下作用能生成D,A 2020-05-17 …
#includemain(){inta=0x7fffffff,b=025;floatf1=123. 2020-05-19 …
设A=B=D=true,C=false,以下逻辑运算表达式值为真的有()。A.(A∧B)∨(C∧D 2020-07-18 …
用Matlab求解方程组?如何用数值法啊?,a,b,c,d是未知量s1=(a/((4*pi*b*c 2020-07-23 …
A,B,C,D四个数的和为59,问A^2+B^2+C^2+D^2,A^3+B^3+C^3+D^3, 2020-07-28 …
EXCEL中如何解决A,A1,A2,A3,A4,.B,B1,B2,B3,B4,.C,C1,C2,C3 2020-10-31 …
多元一次方程求解a=0.1072(a+b+c+d+e)b=0.041(a+b+c+d+e)c=0.2 2020-12-14 …