早教吧作业答案频道 -->数学-->
如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.(1)求证:直线AG垂直平分BC;(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说
题目详情
如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.
(1)求证:直线AG垂直平分BC;
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.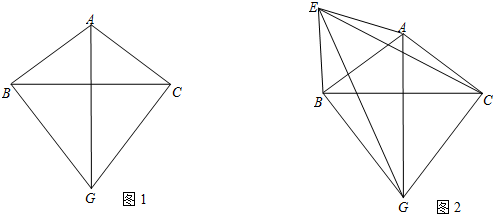
(1)求证:直线AG垂直平分BC;
(2)以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.

▼优质解答
答案和解析
(1)证明:∵△GBC为等边三角形,
∴GB=GC,
∴点G在BC的垂直平分线上,
又∵AB=AC,
∴点A在BC的垂直平分线上,
∴直线AG垂直平分BC;
(2) △EGC能构成直角三角形;理由如下:
∵△GBC和△ABE为等边三角形,
∴GB=BC=GC,EB=BA,∠EBA=∠GBC=∠BGC=∠BCG=60°,
∴∠EBC=∠ABG,
在△EBC和△ABG中,
,
∴△EBC≌△ABG(SAS),
∴∠ECB=∠AGB,
∵GB=GC且AG⊥BC,
∴∠AGB=
∠BGC=30°
∴∠ECB=30°,
∴∠ECG=90°,
即△EGC构成直角三角形.
∴GB=GC,
∴点G在BC的垂直平分线上,
又∵AB=AC,
∴点A在BC的垂直平分线上,
∴直线AG垂直平分BC;
(2) △EGC能构成直角三角形;理由如下:
∵△GBC和△ABE为等边三角形,
∴GB=BC=GC,EB=BA,∠EBA=∠GBC=∠BGC=∠BCG=60°,
∴∠EBC=∠ABG,
在△EBC和△ABG中,
|
∴△EBC≌△ABG(SAS),
∴∠ECB=∠AGB,
∵GB=GC且AG⊥BC,
∴∠AGB=
| 1 |
| 2 |
∴∠ECB=30°,
∴∠ECG=90°,
即△EGC构成直角三角形.
看了 如图1,在△ABC中,AB=...的网友还看了以下:
"三角形ABC在四边形CDEF的平面内",是三角形全在四边形内还是允许有重叠部分三角形全在四边形面 2020-04-27 …
三角形ECD中,EC=12厘米,CD=8厘米,它的面积是长方形ABCF的两倍,求阴影部分三角形AD 2020-06-13 …
我们知道三角形的一条中线能将这个三角形分成面积相等的两个三角形,反之,若经过三角形的一个顶点引一条 2020-07-10 …
设A1A2…An是凸n边形,用n-3条(除端点外)无公共点的对角线,可以将它剖分成三角形,这种剖分 2020-07-12 …
下列说法错误的是()A、三角形三条中线都能平分三角形的面积B、三角形三条角平分线交于三角形内一点C 2020-07-13 …
过三角形的重心作的任意直线平分三角形面积,这是一个假命题,大多给的反例是:过重心且平行于三角形任意 2020-07-29 …
下列正确的是A:平分三角形内角的射线叫做三角形的角平分线B:钝角三角形都是不等腰三角形C:三角形的 2020-08-01 …
按要求分三角形.分成两个直角三角形分成一个钝角三角形和一个锐角三角形. 2020-08-03 …
梯形ABCD被它的对角线BD分成两部分,三角形BCD的面积比三角形ABD的面积大10平方分米已知梯形 2020-11-03 …
在三角形ABC中,角C=90度,AC=3,BC=4,一条直线分三角形的面积为相等的两部分,且夹在AB 2020-12-25 …