早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,AC的垂直平分线交AB于D,交AC于E,AO平分∠BAC交DE于O.(1)若AC=27,△BCD周长等于50,求BC的长;(2)若∠BAC=40°,在BC上存在一点P(P不与B、C重合),使得△BOP是等
题目详情
如图,在△ABC中,AB=AC,AC的垂直平分线交AB于D,交AC于E,AO平分∠BAC交DE于O.
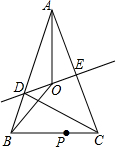
(1)若AC=27,△BCD周长等于50,求BC的长;
(2)若∠BAC=40°,在BC上存在一点P(P不与B、C重合),使得△BOP是等腰三角形,求∠BPO的度数.

(1)若AC=27,△BCD周长等于50,求BC的长;
(2)若∠BAC=40°,在BC上存在一点P(P不与B、C重合),使得△BOP是等腰三角形,求∠BPO的度数.
▼优质解答
答案和解析
(1)∵AC的垂直平分线交AB于D,
∴DA=DC,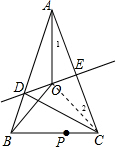
∵△BCD周长等于50,
即BC+BD+CD=50,
∴BC+BD+AD=50,
即BC+AC=50,
∴BC=50-27=23;
(2)连接OC,如图,
∵AB=AC,AO平分∠BAC,
∴AO垂直平分BC,∠1=20°,∠ABC=∠ACB=
(180°-∠BAC)=70°,
∴OB=OC,
∵OE垂直平分AC,
∴OA=OC,
∴∠1=∠2=20°,
∴∠BCO=70°-20°=50°,
∴∠OBC=∠OCB=50°,
当BO=BP时,∠BPO=
(180°-50°)=65°;
当PO=PB时,∠BPO=180°-2×50°=80°,
综上所述,∠BPO的度数为65°或80°.
∴DA=DC,

∵△BCD周长等于50,
即BC+BD+CD=50,
∴BC+BD+AD=50,
即BC+AC=50,
∴BC=50-27=23;
(2)连接OC,如图,
∵AB=AC,AO平分∠BAC,
∴AO垂直平分BC,∠1=20°,∠ABC=∠ACB=
| 1 |
| 2 |
∴OB=OC,
∵OE垂直平分AC,
∴OA=OC,
∴∠1=∠2=20°,
∴∠BCO=70°-20°=50°,
∴∠OBC=∠OCB=50°,
当BO=BP时,∠BPO=
| 1 |
| 2 |
当PO=PB时,∠BPO=180°-2×50°=80°,
综上所述,∠BPO的度数为65°或80°.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
通过学习化学,我们知道了多种途径可以制取氧气.如:A.电解水B.分离空气C.加热高猛酸钾D.分解过 2020-06-27 …
如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形边上.(1) 2020-07-15 …
如图1,在△ABC中,若AD是∠BAC的角平分线,过D点分别作DE⊥AB,DF⊥AC,垂足分别为E 2020-07-22 …
(1)我们知道有多种途径可以获得氧气.如:A.电解水B.分离液态空气C.加热高锰酸钾D.分解过氧化 2020-07-22 …
如图,在矩形OABC中,点A(0,10),C(8,0).沿直线CD折叠矩形OABC的一边BC,使点 2020-07-24 …
已知,在△ABC中,CA=CB=10cm,O为AB的中点,E、F分别在直线AC、BC上,且∠EOF 2020-07-30 …
如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥ 2020-11-03 …
已知正方形ABCD,点E、F分别在射线AB、射线BC上,AE=BF,DE与AF交于点O.(1)如图1 2020-11-03 …
感知:如图①,在菱形ABCD中,AB=BD,点E、F分别在边AB、AD上.若AE=DF,易知△ADE 2020-11-27 …
如图所示:AM∥DN,AE、DE分别平分∠MAD和∠AND,并交于E点.过点E的直线分别交AM、DN 2020-11-28 …