早教吧作业答案频道 -->数学-->
已知正方形ABCD,点E、F分别在射线AB、射线BC上,AE=BF,DE与AF交于点O.(1)如图1,当点E、F分别在射向AB、BC上时,则线段DE于AF的数量关系是,位置关系是.(2)如图2,当点E在线段AB延
题目详情
已知正方形ABCD,点E、F分别在射线AB、射线BC上,AE=BF,DE与AF交于点O.
(1)如图1,当点E、F分别在射向AB、BC上时,则线段DE于AF的数量关系是___,位置关系是___.
(2)如图2,当点E在线段AB延长线上时,将线段AE沿AF进行平移至FG,连接DG.
①依题意将图2不全;
②小亮通过观察,实验提出猜想:在点E运动的过程中,始终有DG2=2AD2+2AE2.
小亮把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种方法:
想法1:连接EG,要证明DG2=2AD2+2AE2,只需证四边形FAEG是平行四边形及△DGE是等腰三角形.
想法2:延长AD、GF交于点H,要证明DG2=2AD2+2AE2,只需证△DGH是直角三角形.
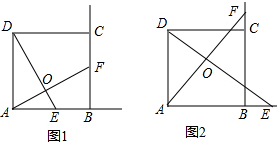
(1)如图1,当点E、F分别在射向AB、BC上时,则线段DE于AF的数量关系是___,位置关系是___.
(2)如图2,当点E在线段AB延长线上时,将线段AE沿AF进行平移至FG,连接DG.
①依题意将图2不全;
②小亮通过观察,实验提出猜想:在点E运动的过程中,始终有DG2=2AD2+2AE2.
小亮把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种方法:
想法1:连接EG,要证明DG2=2AD2+2AE2,只需证四边形FAEG是平行四边形及△DGE是等腰三角形.
想法2:延长AD、GF交于点H,要证明DG2=2AD2+2AE2,只需证△DGH是直角三角形.

▼优质解答
答案和解析
(1)∵四边形ABCD是正方形,
∴∠DAE=∠ABF=90°,DA=AB,
在△DAE和△ABF中,
,
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,即∠AOE=90°,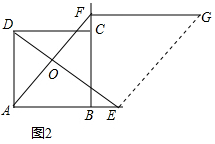
∴DE⊥AF,
故答案为:DE=AF;DE⊥AF;
(2)①补全图形如图所示:
②想法1::连接EG,如图2所示:
由题意得,AE=FG,AE∥FG,
∴四边形FAEG是平行四边形,
∴AF=EG,AF∥EG,
由勾股定理得,DE2=AD2+AE2,
在△DAE和△ABF中,
,
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∴DE=EG,
∵∠ADE+∠AED=90°,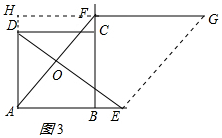
∴∠BAF+∠AED=90°,即∠AOE=90°,
∴DE⊥AF,
∴DE⊥EG,
∴DG2=2DE2,
∴DG2=2AD2+2AE2.
想法2:延长AD、GF交于点H,如图3所示:
由平移的性质得:AE=FG,AE∥FG,
∵AD⊥AB,
∴GH⊥AD,四边形CDHF是矩形,
∴∠H=90°,HF=DC=AD,
∴DG2=GH2+DH2,
∵HG=FG+HF,
∴HG=AE+HF=AE+AD,
同①得:BF=AH,
∵BF=AE,
∴HD=AE-AD,
∴DG2=(AE+AD)2+(AE-AD)2=2AD2+2AE2.
∴∠DAE=∠ABF=90°,DA=AB,
在△DAE和△ABF中,
|
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,即∠AOE=90°,

∴DE⊥AF,
故答案为:DE=AF;DE⊥AF;
(2)①补全图形如图所示:
②想法1::连接EG,如图2所示:
由题意得,AE=FG,AE∥FG,
∴四边形FAEG是平行四边形,
∴AF=EG,AF∥EG,
由勾股定理得,DE2=AD2+AE2,
在△DAE和△ABF中,
|
∴△DAE≌△ABF(SAS),
∴DE=AF,∠ADE=∠BAF,
∴DE=EG,
∵∠ADE+∠AED=90°,

∴∠BAF+∠AED=90°,即∠AOE=90°,
∴DE⊥AF,
∴DE⊥EG,
∴DG2=2DE2,
∴DG2=2AD2+2AE2.
想法2:延长AD、GF交于点H,如图3所示:
由平移的性质得:AE=FG,AE∥FG,
∵AD⊥AB,
∴GH⊥AD,四边形CDHF是矩形,
∴∠H=90°,HF=DC=AD,
∴DG2=GH2+DH2,
∵HG=FG+HF,
∴HG=AE+HF=AE+AD,
同①得:BF=AH,
∵BF=AE,
∴HD=AE-AD,
∴DG2=(AE+AD)2+(AE-AD)2=2AD2+2AE2.
看了已知正方形ABCD,点E、F分...的网友还看了以下:
...一个定义对于向量a(a不等于0),b,如果有一个实数,使b=入a,那么由向量数乘的定义知,a 2020-06-07 …
电磁流量计广泛应用于测量可导电液体(如污水)在管中的流量(在单位时间内通过管内横截面的流体的体积) 2020-07-10 …
通过导体横截面的电荷量同磁通量一样有正负吗?(1)比如一段导线AB1-2S内通向右的电流1A2-3 2020-07-12 …
设点M是线段BC的中点,点A在直线BC外,向量BC的平方等于16,向量AB加向量AC的和的模等于向 2020-07-13 …
我有一个物理学疑问:我的磁铁能把铁球吸来,而运动需要能量,如果能量来自于磁铁,那么磁铁会不会用一段 2020-07-28 …
已知O是直线AB外一点,C、D是线段AB的三等分点,且AC=CD=DB.如果向量OA=3e1,向量 2020-08-01 …
C#关于变量的问题比如说:stringcommand=“iwantto”;string[]word 2020-08-01 …
电磁流量计广泛应用于测量可导电流体(如污水)在管中的流量。为了简化,假设流量计是如图所示的横截面为长 2020-11-01 …
电磁流量计广泛应用于测量可导电液体(如污水)在管中的流量(在单位时间内通过管内横截面的流体的体积), 2020-11-22 …
在“测平均速度的实验”中,用测量物体运动的路程,用测量运动物体通过这段路程的时间,这个实验依据的原理 2020-12-01 …