已知：在△ABC中．AB、AC的垂直平分线分别交BC于点E．F．（1）如图1．∠B=∠C=30°．求∠EAF的度数．（2）如图2．AB≠AC．且90°<∠BAC<180°①若∠BAC=140°．则∠EAF=°：若∠BAC=n&de

Question

已知：在△ABC中．AB、AC的垂直平分线分别交BC于点E．F．
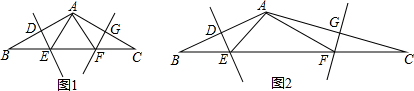
（1）如图1．∠B=∠C=30°．求∠EAF的度数．
（2）如图2．AB≠AC．且90°<∠BAC<180°
①若∠BAC=140°．则∠EAF=___°：若∠BAC=n°．则∠EAF=___
②当∠BAC=___°时．AE⊥AF．
③若BC=a．则△AEF的周长为___．

Answer 1

（1）∵∠B=∠C=30°，
∴∠BAC=180°-30°-30°=120°．
∵AB、AC的垂直平分线分别交BC于点E、F，
∴∠B=∠BAE=30°，∠C=∠CAF=30°，
∴∠EAF=120°-30°-30°=60°；

（2）①∵∠BAC=140°，
∴∠B+∠C=180°-140°=40°．
∵AB、AC的垂直平分线分别交BC于点E，F，
∴∠BAE+∠CAF=40°，
∴∠EAF=140°-40°=100°．
同理，∵∠BAC=n°，
∴∠B+∠C=180°-n°．
∵AB、AC的垂直平分线分别交BC于点E，F，
∴∠BAE+∠CAF=180°-n°，
∴∠EAF=140°-180°+n°=（n-40）°．
故答案为：100，（n-40）°；

②∵AE⊥AF，
∴∠EAF=90°，
∴∠B+∠C+∠BAE+∠CAF=180°-90°=90°．
∵AB、AC的垂直平分线分别交BC于点E，F，
∴∠B=∠BAE，∠C=∠CAF，
∴∠BAE+∠CAF=45°，
∴∠BAC=45°+90°=135°．
故答案为：135；
③∵AB、AC的垂直平分线分别交BC于点E、F，
∴AE=BE，AF=CF，
∴△AEF的周长=AE+AF+EF=BE+CF+EF=BC=a．
故答案为：a．