早教吧作业答案频道 -->数学-->
设是两个互相垂直的单位向量,已知向量且向量,(1)求f(k)的表达式.(2)求f(k)的值域及夹角θ=60°时的k值.(3)在(1)的条件下解关于k的不等式:.
题目详情
设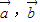 是两个互相垂直的单位向量,已知向量
是两个互相垂直的单位向量,已知向量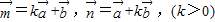 且向量
且向量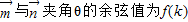 ,
,
(1)求f(k)的表达式.
(2)求f(k)的值域及夹角θ=60°时的k值.
(3)在(1)的条件下解关于k的不等式: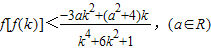 .
.
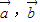 是两个互相垂直的单位向量,已知向量
是两个互相垂直的单位向量,已知向量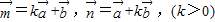 且向量
且向量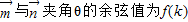 ,
,(1)求f(k)的表达式.
(2)求f(k)的值域及夹角θ=60°时的k值.
(3)在(1)的条件下解关于k的不等式:
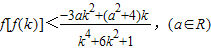 .
.▼优质解答
答案和解析
分析:
(1)由,可求=2k,=,,代入f(k)=cosθ=可求(2)由1+2k2≥2k可得f(k)∈(0,1]结合θ=60°可知cosθ=,可求k(3)由(1)可得f[f(k)]==?,k>0,分类讨论:分a>0时,当a=0时,当a<0时,三种情况分别求解
(1)∵∴,∵∴==2k∵=,同理可得 ∴f(k)=cosθ==(k>0)…(4分)(2)因为1+2k2≥2k当且仅当k=1时等号成立所以f(k)∈(0,1],当θ=60°时,cosθ=∴ (8分)(3)由(1)可得f[f(k)]=f()==?4k3+4k<-3ak2+(4+a2)k?k(4k2+3ak-a2)<0?,∵k>0当a>0时,解可得0<k<当a=0时,解为k<0且k>0,此时k不存在当a<0时,解为0<k<-a综上所述:当a>0时,解集为{k|0<k<};当a=0时,解集为?当a<0时,解集为{k|0<k<-a}(12分)
点评:
本题主要考查了向量的数量积的应用,向量夹角公式的应用,及不等式的求解,属于综合试题
分析:
(1)由,可求=2k,=,,代入f(k)=cosθ=可求(2)由1+2k2≥2k可得f(k)∈(0,1]结合θ=60°可知cosθ=,可求k(3)由(1)可得f[f(k)]==?,k>0,分类讨论:分a>0时,当a=0时,当a<0时,三种情况分别求解
(1)∵∴,∵∴==2k∵=,同理可得 ∴f(k)=cosθ==(k>0)…(4分)(2)因为1+2k2≥2k当且仅当k=1时等号成立所以f(k)∈(0,1],当θ=60°时,cosθ=∴ (8分)(3)由(1)可得f[f(k)]=f()==?4k3+4k<-3ak2+(4+a2)k?k(4k2+3ak-a2)<0?,∵k>0当a>0时,解可得0<k<当a=0时,解为k<0且k>0,此时k不存在当a<0时,解为0<k<-a综上所述:当a>0时,解集为{k|0<k<};当a=0时,解集为?当a<0时,解集为{k|0<k<-a}(12分)
点评:
本题主要考查了向量的数量积的应用,向量夹角公式的应用,及不等式的求解,属于综合试题
看了 设是两个互相垂直的单位向量,...的网友还看了以下:
如图,正比例函数y=2x与反比例函数y=kx(k>0)的图象相交于A、C两点,过点A作AD垂直x轴 2020-04-08 …
如图,P是反比例函数y=kx(k>0)的图象上的任意一点,过P作x轴的垂线,垂足为M,已知△POM 2020-04-08 …
设向量a=(cosa,sina),b=(cosb,sinb),且a和b满足|ka+b|=根号3|a 2020-05-15 …
垂直直线方程过点(1,1)的直线与直线y=0垂直的直线方程式?今天成人高考,上面一道数学题做不来, 2020-05-17 …
过点B(-2,0)且与X轴垂直求直线方程这个有点想不通与X轴垂直的话也就是斜率不存在吧?公式Y-Y 2020-05-23 …
在平面直角坐标系中点O为坐标原点.反比例函数Y=X分之K.图像经过第一像线点点A(2,M).过点A 2020-05-23 …
八年级关于反比例函数的问题如图,直线y=mx与双曲线y=k/x交于点A,B.过点A作AM垂直x轴, 2020-06-06 …
已知关于x,y的二元二次方程x∧2+y∧2+2x-4y+k=0(k∈R)表示圆C.是否存在实数K使 2020-06-14 …
如图所示,P是反比例函数y=x分之k(k大于0)的图像上的任一点,过P作ix轴的垂线,垂足为Q,已 2020-06-27 …
k的几何含义:反比例函数y=k/x(k≠0)中比例系数k的几何意义,即过双曲线y=k/x上任意一点 2020-06-27 …