如图，点A在反比例函数y=6x图象第一象限的分支上，连结AO并延长交另一分支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第四象限，AC与x轴交于点D，若△OAD与△BCD的面积相等，则点A的横

Question

如图，点A在反比例函数y=

(6)/(x)图象第一象限的分支上，连结AO并延长交另一分支于点B，以AB为斜边作等腰直角三角形ABC，顶点C在第四象限，AC与x轴交于点D，若△OAD与△BCD的面积相等，则点A的横坐标是（　　）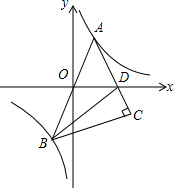

A.

√(3)

B. 2

C.

√(6)

D. 2

√(3)

Answer 1

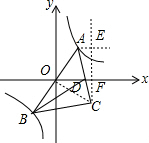连接OC，分别过点A、C作x、y轴的平行线交于E点，CE交x轴于F点，如图：
由反比例的性质可知，A、B两点关于中心O对称，即OA=OB，
又∵△ACB为等腰直角三角形，
∴CO⊥AB，且OC=OA．设直线AB的解析式为y=ax（a>0），则OC的解析式为y=-(1)/(a)x，
设点A（m，am），点C（an，-n），
∵OA=OC，即m²+（am）²=（an）²+n²，
解得n=±m，
∵A在第一象限，C在第三象限，
∴n=m>0，
即C（am，-m）．
∵AE∥x轴，CE∥y轴，
∴∠CDF=∠CAE，∠CFD=∠CEA=90°，
∴△CDF∽△CAE，
∴(CF)/(CE)=(CD)/(CA)，
又∵△OAD与△BCD的面积相等，△OAD与△BOD的面积相等，
∴S_△ABD=2S_△BCD，
∴(AD)/(CD)=2，
∵AC=AD+CD，
∴(CF)/(CE)=(CD)/(CA)=(1)/(3)，
∵点A（m，am），点C（am，-m），
∴点E（am，am），点F（am，0），
∴(CF)/(CE)=(0-(-m))/(am-(-m))=(1)/(a+1)=(1)/(3)，
即a=2．
∵点A（m，am）在反比例函数y=(6)/(x)的图象上，且a=2，
∴2m²=6，解得m=±√(3)，
∵m>0，
∴m=√(3)，
∴点A的横坐标是√(3)，
故选A．