早教吧作业答案频道 -->数学-->
在平面几何的学习过程中,我们经常会研究角和线之间的关系.(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系时,a∥b;(2)如图②,在(1)中,作射线B
题目详情
在平面几何的学习过程中,我们经常会研究角和线之间的关系.
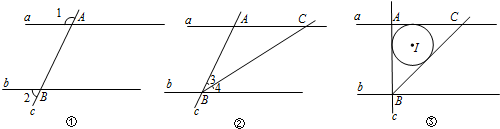
(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系___时,a∥b;
(2)如图②,在(1)中,作射线BC,与直线a的交点为C,当∠3、∠4满足何种数量关系时,AB=AC?证明你的结论;
(3)如图③,在(2)中,若∠BAC=90°,AB=2, I为△ABC的内切圆.
①求 I的半径;
②P为直线a上一点,若 I上存在两个点M、N,使∠MPN=60°,直接写出AP长度的取值范围.

(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系___时,a∥b;
(2)如图②,在(1)中,作射线BC,与直线a的交点为C,当∠3、∠4满足何种数量关系时,AB=AC?证明你的结论;
(3)如图③,在(2)中,若∠BAC=90°,AB=2, I为△ABC的内切圆.
①求 I的半径;
②P为直线a上一点,若 I上存在两个点M、N,使∠MPN=60°,直接写出AP长度的取值范围.
▼优质解答
答案和解析
(1)∠1+∠2=180°,
故答案为:∠1+∠2=180°;
(2)当∠3=∠4时,AB=AC,
证明:∵a∥b,
∴∠ACB=∠4,
又∵∠3=∠4,
∴∠ACB=∠3,
∴AB=AC;
(3)①由(2)得AB=AC,
又∵∠BAC=90°,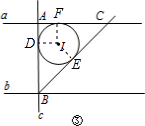
∴△ABC是等腰直角三角形.
∵AB=2,
∴AC=2.
∴在Rt△ABC中,BC=
=2
.
设D、E、F分别为边AB、BC、AC上的切点,
连接ID、IE、IF,
∵ I为△ABC的内切圆,
∴ID⊥AB、IE⊥BC、IF⊥AC.
∴AD=AF,BD=BE,CE=CF.
∵∠BAC=90°,
∴四边形ADIF是矩形.
∵ID=IF,
∴矩形ADIF是正方形.
∴r=AD=
=2-
.
∴ I的半径为2-
;
②当点P在射线AC上时,0≤AP≤2
-
+2-
,
当点P在射线AC的反向延长线上时,0≤AP≤2
-
-2+
.
故答案为:∠1+∠2=180°;
(2)当∠3=∠4时,AB=AC,
证明:∵a∥b,
∴∠ACB=∠4,
又∵∠3=∠4,
∴∠ACB=∠3,
∴AB=AC;
(3)①由(2)得AB=AC,
又∵∠BAC=90°,

∴△ABC是等腰直角三角形.
∵AB=2,
∴AC=2.
∴在Rt△ABC中,BC=
| AB2+AC2 |
| 2 |
设D、E、F分别为边AB、BC、AC上的切点,
连接ID、IE、IF,
∵ I为△ABC的内切圆,
∴ID⊥AB、IE⊥BC、IF⊥AC.
∴AD=AF,BD=BE,CE=CF.
∵∠BAC=90°,
∴四边形ADIF是矩形.
∵ID=IF,
∴矩形ADIF是正方形.
∴r=AD=
| AB+AC-BC |
| 2 |
| 2 |
∴ I的半径为2-
| 2 |
②当点P在射线AC上时,0≤AP≤2
| 3 |
| 6 |
| 2 |
当点P在射线AC的反向延长线上时,0≤AP≤2
| 3 |
| 6 |
| 2 |
看了 在平面几何的学习过程中,我们...的网友还看了以下:
数学带余除法车苹果五千多个,按十个袋一袋,装到最后少一个,按九个八个……二个都少一个,苹果多少个一 2020-06-02 …
几道高中数学必修3随机抽样习题答案,第一题用随机数表法从100名学生(其中男生25人)中抽选20人 2020-06-03 …
100个杯子杯口朝上排成一行,顺次从1到100编号,有100位学生,第一位学生把编号能被1整除的杯 2020-06-27 …
几道数学问题:1,从9名同学中选一名当班长,4名当班委,一共有几种选法?2,69,90,125被A除 2020-10-30 …
初三数学几何1平行四边形ABCD中AC=根号2AB.求证角ABD=角DAC(要过程)2已知矩形ABC 2020-11-03 …
珍珍是个温顺的女孩,与人谈话时脸红心跳,结结巴巴,越来越不敢说话了,朋友很少。上中学后,见到同学几乎 2020-11-05 …
六年级上学期的边玩边学答案1.古希腊著名的数学家丢番图的生平历史几乎没有被记载下来,后人仅从他的很特 2020-11-22 …
初二数学几何1.如图,在Rt△ABC中,∠C90°,AC=BC,AD平分∠CAB,DE⊥AB于E,若 2020-12-01 …
福建某中学学生小王在2008年高考中以优异的成绩被东北某名牌大学录取,学费及各种费用上万元。准备出发 2020-12-22 …
英语翻译1这位导演为了寻找能担任一部大片主演的演员,在电影学院呆了好几天2到现在为止,他选出了三个学 2021-01-12 …