早教吧作业答案频道 -->数学-->
我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线
题目详情
我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线
-
=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=
x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积___.
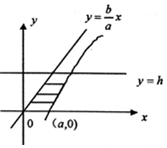
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |

▼优质解答
答案和解析
y=m,是一个圆环其面积
S=π(AC2-BC2)
∵线
-
=1⇒AC2=a2+
m2,
同理BC2=
m2
∴AC2-BC2=a2,由祖暅原理知,此旋转体的体积,等价于一个半径为a,高为h的柱体的体积为a2hπ.
故答案为:a2hπ.
S=π(AC2-BC2)
∵线
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| b2 |
同理BC2=
| a2 |
| b2 |
∴AC2-BC2=a2,由祖暅原理知,此旋转体的体积,等价于一个半径为a,高为h的柱体的体积为a2hπ.
故答案为:a2hπ.
看了 我们在学习立体几何推导球的体...的网友还看了以下:
已知二次函数F(x)=a(a+1)x*X-(2a+1)x+1,a∈N+1.求函数F(X)的图像与X 2020-05-13 …
我们在学习立体几何推导球的体积公式时,用到了祖日恒原理:即两个等高的几何体,被等高的截面所截,若所 2020-06-14 …
如图所示,AB与BC被AD所截得的内错角是;DE与AC被AD所截得的内错角是;∠1与∠4是直线被直 2020-07-23 …
下列说法正确的是[]A.如果线段AB与线段CD不相交,则线段AB与CD平行.B.两条直线被第三条直 2020-07-23 …
如图所示,AB与BC被AD所截得的内错角是;DE与AC被AD所截得的内错角是;∠1与∠4是直线被直 2020-07-23 …
已知园x方+y方+6x-8y+25=r方与x轴相切,求这个圆截y轴所得的弦长已知圆C与y轴相切,圆 2020-07-26 …
初一数学1.∠B与∠FAC是直线、被直线所截得的2.∠BAC与是直线AB,CE被直线所截得得内错角 2020-07-29 …
如图,直线l1、l2、l3两两相交,则对于∠1、∠2,下列说法正确的是()A.∠1、∠2是直线l1 2020-08-01 …
有下列两个命题:命题1:两条平行线被第三条直线所截得的内错角的平分线互相平行;命题2:两条直线被第 2020-08-01 …
我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截 2020-08-02 …