早教吧作业答案频道 -->数学-->
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.(1)若DE∥平面A1MC1,求CEEB;(2)求证:平面B1MC1⊥平面A1MC1.
题目详情
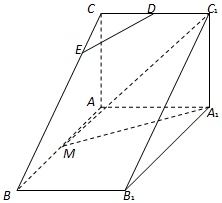
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
(1)若DE∥平面A1MC1,求
;
(2)求证:平面B1MC1⊥平面A1MC1.

(1)若DE∥平面A1MC1,求
| CE |
| EB |
(2)求证:平面B1MC1⊥平面A1MC1.
▼优质解答
答案和解析
(1)取BC中点为N,连结MN,C1N,
∵M,N分别为AB,CB中点∴MN∥AC∥A1C1,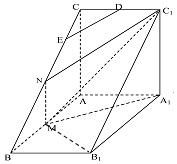
∴A1,M,N,C1四点共面,
且平面BCC1B1∩平面A1MNC1=C1N,
又DE⊂平面BCC1B1,且DE∥平面A1MC1,
∴DE∥C1N,
∵D为CC1的中点,∴E是CN的中点,∴
=
. …(6分)
证明:(2)连结B1M,
∵三棱柱ABC-A1B1C1为直三棱柱,∴AA1⊥平面ABC,
∴AA1⊥AB,即四边形ABB1A1为矩形,且AB=2AA1,
∵M是AB的中点,∴B1M⊥A1M,
又A1C1⊥平面ABB1A1,∴A1C1⊥B1M,
从而B1M⊥平面A1MC1,
∵B1M⊂平面B1MC1,∴平面B1MC1⊥平面A1MC1.…(12分)
∵M,N分别为AB,CB中点∴MN∥AC∥A1C1,

∴A1,M,N,C1四点共面,
且平面BCC1B1∩平面A1MNC1=C1N,
又DE⊂平面BCC1B1,且DE∥平面A1MC1,
∴DE∥C1N,
∵D为CC1的中点,∴E是CN的中点,∴
| CE |
| EB |
| 1 |
| 3 |
证明:(2)连结B1M,
∵三棱柱ABC-A1B1C1为直三棱柱,∴AA1⊥平面ABC,
∴AA1⊥AB,即四边形ABB1A1为矩形,且AB=2AA1,
∵M是AB的中点,∴B1M⊥A1M,
又A1C1⊥平面ABB1A1,∴A1C1⊥B1M,
从而B1M⊥平面A1MC1,
∵B1M⊂平面B1MC1,∴平面B1MC1⊥平面A1MC1.…(12分)
看了 如图,直三棱柱ABC-A1B...的网友还看了以下:
C++构造一个圆柱体的类构造一个圆柱体的类,定义该类对象a,再定义一个和a同底等高的圆柱体b,计算 2020-04-27 …
如图,用高为6cm,底面直径为4cm的圆柱A的侧面积展开图,再围成不同于A的另一个圆柱B,则圆柱B 2020-05-14 …
如图,用高为6cm,底面直径为4cm的圆柱A的侧面积展开图,再围成不同于A的另一个圆柱B,则圆柱B 2020-07-10 …
圆柱体A的底面积是50cm2,圆柱体B的底面积是30cm2,圆柱体B的质量是6kg.把它们如图所示 2020-07-18 …
若圆柱的体积是2πa³+3πa³底面半径为a,请你试着求出这个圆柱体的高,还有↓1、若圆柱的体积是 2020-07-30 …
如图所示,上端封闭、下端开口内径均匀的玻璃管,管长L=100cm,其中有一段长h=15cm的水银柱 2020-07-31 …
如图所示,上端封闭、下端开口内径均匀的玻璃管,管长L=100cm,其中有一段长h=15cm的水银柱 2020-07-31 …
如图所示,圆柱体A和圆柱体B放在水平地面上.圆柱体A对地面的压强为рA,圆柱体B对地面的压强为рB 2020-07-31 …
如图,可视为质点的小球A,B用不可伸长的细软轻线连接,跨过固定在地面上半径为R有光滑圆柱,A的质量为 2020-11-10 …
(2013•太原二模)如图所示,内径均匀的玻璃管长L=100cm,其中有一段长h=15cm的水银柱把 2020-11-11 …