早教吧作业答案频道 -->数学-->
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.(1)证明:平面AEF⊥平面B1BCC1;(2)设AB的中点为D,且CD=A1D,求三棱锥A1-AEF的体积.
题目详情
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.
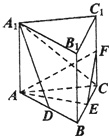
(1)证明:平面AEF⊥平面B1BCC1;
(2)设AB的中点为D,且CD=A1D,求三棱锥A1-AEF的体积.

(1)证明:平面AEF⊥平面B1BCC1;
(2)设AB的中点为D,且CD=A1D,求三棱锥A1-AEF的体积.
▼优质解答
答案和解析
证明:(1)∵三棱柱ABC-A1B1C1是直三棱柱,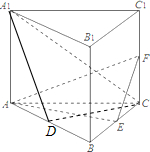
∴B1B⊥底面ABC,则AE⊥BB1,
又E是正三角形ABC的边BC的中点,
∴AE⊥BC,
又B1B∩BC=B,
因此AE⊥平面B1BCC1,而AE⊂平面AEF,
∴平面AEF⊥平面B1BCC1;
(2)在正三角形ABC中,由AB=BC=AC=2,得CD=
,
∵CD=A1D,
∴A1D=
,
在Rt△AA1D中,AA1=
=
,
∴三棱锥A1-AEF的体积=三棱锥E-A1AF的体积=
×
×
×2×
=
.

∴B1B⊥底面ABC,则AE⊥BB1,
又E是正三角形ABC的边BC的中点,
∴AE⊥BC,
又B1B∩BC=B,
因此AE⊥平面B1BCC1,而AE⊂平面AEF,
∴平面AEF⊥平面B1BCC1;
(2)在正三角形ABC中,由AB=BC=AC=2,得CD=
| 3 |
∵CD=A1D,
∴A1D=
| 3 |
在Rt△AA1D中,AA1=
| 3-1 |
| 2 |
∴三棱锥A1-AEF的体积=三棱锥E-A1AF的体积=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 6 |
看了 如图,直三棱柱ABC-A1B...的网友还看了以下:
初二数学,急求!1用10的负整数幂填空:(1)1秒是1微妙的1000000倍,则1微妙=秒(2)1 2020-05-13 …
有一个高为1.1米的正方体水池刚好能装满28桶水,已知水桶是一个圆柱体,...有一个高为1.1米的 2020-05-20 …
1.观察下面几个关于平方和的有趣等式:1的平方+4的平方+6的平方+7的平方=2的平方+3的平方+ 2020-06-04 …
一、我们知道1/1×2=1/1-1/2=1/2,1/2×3=1/2-1/3=1/6验证:1/3×4 2020-07-17 …
直角三角形1:1:根号2请问各路高手:直角三角形三个角分别为30°60°90°我想问的是:1:1: 2020-07-22 …
寻找规律解数学题1/1*2=1-1/22/2*3=1/2-1/31/3*4=1/3-1/4……计算 2020-07-22 …
由下列各式:1>1/2,1+1/2+1/3>1有下列各式:1>1/2;1+1/2+1/3>1;1+1 2020-10-30 …
计算一道数学题,(1+1/2)×(1+1/3)×(1+1/4)×(1+1/5)×(1+1/6)×(1 2020-11-30 …
观察下列算式:1-1/2的平方=1-1/4=3/4=1/2*3/2;1-1/3的平方=1-1/9=8 2020-12-23 …
观察下列算式:1-1/2的平方=1-1/4=3/4=1/2*3/2;1-1/3的平方=1-1/9=8 2020-12-23 …