早教吧作业答案频道 -->数学-->
已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=3,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).(1)证明:平面DEG∥平面ABF;(2)求
题目详情
已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=
,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).
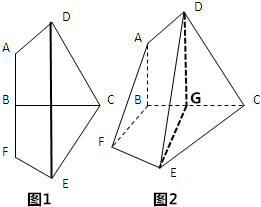
(1)证明:平面DEG∥平面ABF;
(2)求多面体ABC-DEF的体积.
| 3 |

(1)证明:平面DEG∥平面ABF;
(2)求多面体ABC-DEF的体积.
▼优质解答
答案和解析
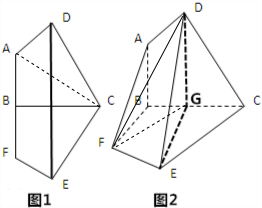 (1)证明:由平面图形,可得DG∥AB,GE∥BF,
(1)证明:由平面图形,可得DG∥AB,GE∥BF,
∵DG⊄平面ABF,AB⊂平面ABF,
∴DG∥平面ABF.
同理GE∥平面ABF.
∵DG∩GE=G,
∴平面DEG∥平面ABF;
(2) 图(1),连接AC,则由勾股定理可得AC=2,
∴∠BCD=60°,
∴DG=
,BG=
.
图(2),连接DF,GF,则多面体ABC-DEF的体积=VF-ABGD+VF-DGE=
×
×
×1+
×
×
×
=
.
 (1)证明:由平面图形,可得DG∥AB,GE∥BF,
(1)证明:由平面图形,可得DG∥AB,GE∥BF,∵DG⊄平面ABF,AB⊂平面ABF,
∴DG∥平面ABF.
同理GE∥平面ABF.
∵DG∩GE=G,
∴平面DEG∥平面ABF;
(2) 图(1),连接AC,则由勾股定理可得AC=2,
∴∠BCD=60°,
∴DG=
| 3 |
| 2 |
| ||
| 2 |
图(2),连接DF,GF,则多面体ABC-DEF的体积=VF-ABGD+VF-DGE=
| 1 |
| 3 |
1+
| ||
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
7
| ||
| 12 |
看了 已知平面五边形ADCEF关于...的网友还看了以下:
已知集合A={第一象限角},B={锐角},C={小于90°的角},则下列关系中正确的是:A、A=B 2020-05-16 …
现有短周期元素A、B、C、D。A元素M层上有2对成对电子,D与A在周期表中同一主族。由A、B与D组 2020-07-07 …
已知,如图B、D、A在一直线上,且∠D=∠E,∠ABE=∠D+∠E,BC是∠ABE的平分线,求证: 2020-07-11 …
一条化学题目~求高手A和X在高温下生成C和D~A在高中一个有U型馆的装置里做电极~点解G的溶液生成 2020-07-22 …
一道关于正方形的行程问题~有一个边长为90米的正方形,沿着a.b.c.d.(a在左上角,b在左下角 2020-07-25 …
(2014•汕尾)如图,已知抛物线y=38x2-34x-3与x轴的交点为A、D(A在D的右侧),与 2020-07-26 …
若三棱锥S-ABC的顶点S在底面上的射影H在△ABC的内部,且是△ABC的垂心,则()A.三条侧棱 2020-07-30 …
1·国际地理奥林匹克考察小组在厄瓜多尔的赤道地区做了实验,一个水杯,下面有木塞塞住,乘水,水面上有花 2020-11-03 …
如图,折线ABC是一个路灯的示意图,AB垂直于地面,线段AB与线段BC所成的角∠ABC=120°,在 2020-11-21 …
某校平面图的一部分如图所示,则对点A、B的方位的说法基本正确的是()A.点A在点B的北偏西30°方向 2021-01-02 …