早教吧作业答案频道 -->数学-->
如图,有两条互相平行的直线l1,l2,点A,B在直线l1上,点D,C在直线l2上,连接AD,BC.已知∠ADC=90°,AB=3,DC=6,BC=5.点E是线段DC上任意一点,点F在线段AB的延长线上,且AE=AF,连接EF,与线
题目详情
如图,有两条互相平行的直线l1,l2,点A,B在直线l1上,点D,C在直线l2上,连接AD,BC.已知∠ADC=90°,AB=3,DC=6,BC=5.点E是线段DC上任意一点,点F在线段AB的延长线上,且AE=AF,连接EF,与线段BC相交于点G.
(1)求线段AD的长;
(2)求线段BF最大值与最小值;
(3)连接BE,FC,当BE∥CF时,求BF的长.
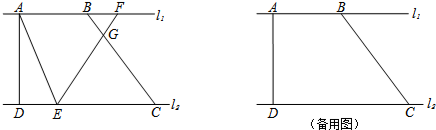
(1)求线段AD的长;
(2)求线段BF最大值与最小值;
(3)连接BE,FC,当BE∥CF时,求BF的长.
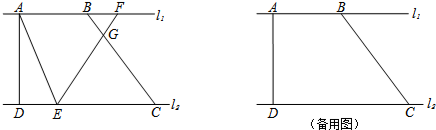
▼优质解答
答案和解析
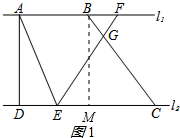 (1)作BM⊥CD于M,如图1所示:
(1)作BM⊥CD于M,如图1所示:
∵∠ADC=90°,
∴BM∥AD,
∵l1∥l2,
∴四边形ADMB是矩形,
∴AD=BM,DM=AB=3,
∴CM=DC-DM=3,
∴AD=BM=
=
=4;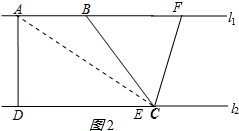
(2)当点E与C重合时,BF有最大值,连接AC,如图2所示:
则AE=AC=
=
=2
,
∴AF=AE=2
,BF的最大值=2
-3;
当点E与D重合时,BF有最小值,
∵AF=AE=AD=4,
∴BF的最小值=4-3=1;
(3)如图3所示:当BE∥CF时,四边形BECF是平行四边形,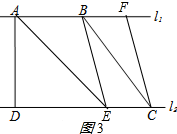
∴BF=CE,
设BF=CE=x,则AE=AF=AB+BF=3+x,DE=DC-CE=6-x,
在Rt△ADE中,由勾股定理得:AD2+DE2=AE2,
即42+(6-x)2=(x+4)2,
解得:x=1.8,
即BF的长为1.8.
 (1)作BM⊥CD于M,如图1所示:
(1)作BM⊥CD于M,如图1所示:∵∠ADC=90°,
∴BM∥AD,
∵l1∥l2,
∴四边形ADMB是矩形,
∴AD=BM,DM=AB=3,
∴CM=DC-DM=3,
∴AD=BM=
| BC2-CM2 |
| 52-32 |

(2)当点E与C重合时,BF有最大值,连接AC,如图2所示:
则AE=AC=
| AD2+DC2 |
| 42+62 |
| 13 |
∴AF=AE=2
| 13 |
| 13 |
当点E与D重合时,BF有最小值,
∵AF=AE=AD=4,
∴BF的最小值=4-3=1;
(3)如图3所示:当BE∥CF时,四边形BECF是平行四边形,

∴BF=CE,
设BF=CE=x,则AE=AF=AB+BF=3+x,DE=DC-CE=6-x,
在Rt△ADE中,由勾股定理得:AD2+DE2=AE2,
即42+(6-x)2=(x+4)2,
解得:x=1.8,
即BF的长为1.8.
看了 如图,有两条互相平行的直线l...的网友还看了以下:
如图,抛物线y=ax的平方+bx+c的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.( 2020-05-16 …
如图,抛物线y=-x2+2x+3的顶点为C,交x轴于A、B两点,交Y轴于点D(1)求A、C、D三个 2020-05-16 …
如图所示,OA是圆O的半径,以OA为直径的圆C与圆O的玄AB相交于点D.1.说明线段BD与AD的大 2020-07-02 …
如图,在平面直角坐标系xOy中,已知F1,F2分别是椭圆E:=1(a>b>0)的左、右焦点,A,B 2020-07-06 …
已知直线y=2x+4与x轴的交点为A,与y轴的交点为B,点D(1,6),E(-3,-2)在这条直线 2020-07-20 …
已知两点D(1,-1),E(-1,-4),试在直线L上确定一点Q,使点Q到D、E两点的距离之和最小 2020-07-20 …
圆C经过点A(1,-1)、B(-1,1)且圆心C在直线x+y-2=0上过点D(-1,-1)的直线l 2020-07-26 …
、已知在三角形ABC中,AB=AC,过点A的直线与三角形ABC的外接圆O于点D,.1、已知在三角形 2020-07-31 …
如图,抛物线y=x²-2x-3与x轴交于A、B两点,与y轴交于点C,顶点为点D.(1)求出A、B、C 2020-11-01 …
RT△OAB其中角AOB=90°OA=2OB=4将它放置在坐标系中折叠折痕与OB交点C与边AB交点D 2020-12-25 …