早教吧作业答案频道 -->数学-->
如图,已知抛物线y=ax2+bx+c经过原点O,它的顶点坐标为(5,254),在抛物线内作矩形ABCD,使顶点C,D落在抛物线上,顶点A,B落在x轴上.(1)求抛物线对应的函数表达式;(2)若AB=6,求AD
题目详情
如图,已知抛物线y=ax2+bx+c经过原点O,它的顶点坐标为(5,
),在抛物线内作矩形ABCD,使顶点C,D落在抛物线上,顶点A,B落在x轴上.
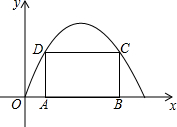
(1)求抛物线对应的函数表达式;
(2)若AB=6,求AD的长;
(3)设矩形ABCD的周长为l,求l的最大值.
| 25 |
| 4 |

(1)求抛物线对应的函数表达式;
(2)若AB=6,求AD的长;
(3)设矩形ABCD的周长为l,求l的最大值.
▼优质解答
答案和解析
(1)根据坐标系可知此函数顶点坐标为(5,
),且图象过(0,0)点,
代入顶点式得:
y=a(x-5)2+
,
将(0,0)代入解析式得:
∴0=a(0-5)2+
,
解得:a=-0.25,
∴y=-0.25(x-5)2+
;
(2)∵此函数顶点坐标为(5,
),且图象过(0,0)点,
∴图象与x轴另一交点为:(10,0),
当AB=6时,
∴AO=(10-6)÷2=2,
∴x=2代入解析式得:
y=-0.25(2-5)2+6.25;
y=4,
∴AD=4;
(3)假设AO=x,可得AB=10-2x,
∴AD=-0.25(x-5)2+6.25;
∴矩形ABCD的周长为l为:l=2[-0.25(x-5)2+6.25]+2(10-2x)=-0.5x2+x+20,
∴l的最大值为:
=
=20.5.
| 25 |
| 4 |
代入顶点式得:
y=a(x-5)2+
| 25 |
| 4 |
将(0,0)代入解析式得:
∴0=a(0-5)2+
| 25 |
| 4 |
解得:a=-0.25,
∴y=-0.25(x-5)2+
| 25 |
| 4 |
(2)∵此函数顶点坐标为(5,
| 25 |
| 4 |
∴图象与x轴另一交点为:(10,0),
当AB=6时,
∴AO=(10-6)÷2=2,
∴x=2代入解析式得:
y=-0.25(2-5)2+6.25;
y=4,
∴AD=4;
(3)假设AO=x,可得AB=10-2x,
∴AD=-0.25(x-5)2+6.25;
∴矩形ABCD的周长为l为:l=2[-0.25(x-5)2+6.25]+2(10-2x)=-0.5x2+x+20,
∴l的最大值为:
| 4ac-b2 |
| 4a |
| -40-1 |
| -2 |
看了 如图,已知抛物线y=ax2+...的网友还看了以下:
如图,△ABC经过某种变换得到的图形,点A与点P,点B与点Q,点C与点R是对应点,观察它们之间的关 2020-05-16 …
为什么说成中心对称图形函数Y=tanx的图像,其对称中心坐标为(kpi/2,0)k属于Z,而不是( 2020-06-27 …
将△ABC的三个顶点的横坐标不变,纵坐标乘以-1,则所得图形()A.与原图形关于x轴对称B.与原图 2020-07-31 …
将△ABC的三个顶点坐标的横坐标都乘以-1,并保持纵坐标不变,则所得图形与原图形的关系是()A.关 2020-07-31 …
坐标坐标(520:25:50)将⊿ABC的三个顶点坐标的横坐标都×-1,纵坐标不变,则所得图形与原 2020-07-31 …
如果一个图形绕原点O旋转180°,得到新图形的对应顶点的横坐标与原图形对应顶点的横坐标,纵坐标. 2020-08-02 …
函数的对称函数y=-e^x的图象1.与y=e^x的图象关于y轴对称2.与y=e^x的图象关于坐标原点 2020-11-11 …
如图,在直角坐标平面内,已知点A的坐标(-5,0),(1)图中B点的坐标是;(2)点B关于原点对称的 2020-11-11 …
材料:我国幅员辽阔,南北、东西自然差异较大。受各种自然环境要素的影响,各地形成了独特的自然环境特征, 2020-12-10 …
在坐标平面上有一个轴对称图形,其中A(3,-52)和B(3,-112)是图形上的一对对称点,若此图形 2021-01-12 …