早教吧作业答案频道 -->数学-->
某三棱椎的三视图如图所示,则其体积为.
题目详情
某三棱椎的三视图如图所示,则其体积为___.
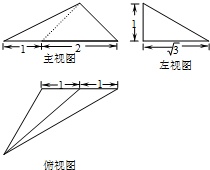

▼优质解答
答案和解析
根据三视图可知几何体是一个三棱锥,
底面是一个三角形:即俯视图:底是2、高是侧视图的底边
,
三棱锥的高是侧视图和正视图的高1,
∴几何体的体积V=
×
×2×
×1=
,
故答案为:
.
底面是一个三角形:即俯视图:底是2、高是侧视图的底边
| 3 |
三棱锥的高是侧视图和正视图的高1,
∴几何体的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
故答案为:
| ||
| 3 |
看了 某三棱椎的三视图如图所示,则...的网友还看了以下:
高斯公式求球体的曲面积分,3Q!设S为球面x方+y方+z方=a方 的外侧,S所围成的球体G的体积V 2020-05-16 …
三重积分先二后一截面法问题.求∫∫∫3zdv,积分区域是Ω是z=1-x²-¼y²(0≦z≦1),我 2020-05-17 …
被积函数为1的话,二重积分或第一类曲面积分代表被积区域面积,第一类曲线积分代表曲线长度,三重积分代 2020-06-14 …
(2012•河南三模)椎实螺是雌雄同体的动物,一般进行异体受精,但分开饲养时,它们进行自体受精.已 2020-06-21 …
两个较小的正方体积木分别粘在一个大正方体积木的两个面上,构成如图所示的立体图形,其中,每个小积木粘 2020-07-07 …
二重积分的积分中值定理,如何确定其面积对应的正负号如二重积分的区域在第四象限,那么它的那块面积的正 2020-07-26 …
1、一个形状如圆椎的冰淇淋纸筒,其底面直径为6cm,母线长5cm,围成这样的冰淇淋纸筒所需纸片面积 2020-07-31 …
关于三重积分∫∫∫xyzdxdydz=0V为半径为1的球体是不是只要:如果积分区域关于平面(如xo 2020-07-31 …
请问高数中:坐标轮转法的前提条件是什么是不是这样,如果是二重积分的话,如果积分曲面关于x轴,y轴都 2020-08-02 …
这形状到底叫什么啊,三角体?椎体?还是什么玩意=然后求它体积公式.就跟三明治一样的形状.3个长方形和 2020-12-06 …