早教吧作业答案频道 -->数学-->
已知:正方形ABCD内一点E,连接EA、EB、EC.(1)若EA2+EC2=2EB2,请说明点E必在对角线AC上.(2)若EA+EB+EC的最小值为2(3+1),求正方形ABCD的边长.
题目详情
已知:正方形ABCD内一点E,连接EA、EB、EC.
(1)若EA2+EC2=2EB2,请说明点E必在对角线AC上.
(2)若EA+EB+EC的最小值为
(
+1),求正方形ABCD的边长.
(1)若EA2+EC2=2EB2,请说明点E必在对角线AC上.
(2)若EA+EB+EC的最小值为
| 2 |
| 3 |

▼优质解答
答案和解析
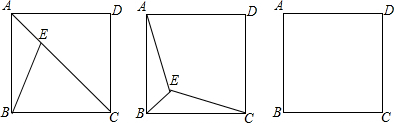
(1)证明:如图1中,将△ABE绕点B顺时针旋转90°得△CBE′,连接EE′.
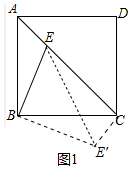
∵BE=BE′,∠EBE′=90°,AE=CE′,
∴EE′=
BE,
∵EA2+EC2=2EB2,
∴CE′2+EC2=EE′2,
∴∠ECE′=90°,
∴∠ECB+∠BCE′=∠ECB+∠BAE=90°,
∴A、E、C共线,
∴点E在正方形ABCD的对角线上.
(2) 如图2中,将△ABE绕点B逆时针旋转60°得△A′BE′,连结A′C,作A′H⊥BC于H.
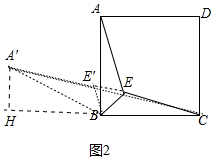
∵△ABE绕点B逆时针旋转60°得△A′BE′,
∴BE=BE′,∠EBE′=60°,
∴△EBE′为等边三角形,
∴EE′=BE,
∴A′E′=AE,BA′=BA=2,∠ABA′=60°,
∵A′E′+E′E+EC≥A′C,
∴AE+BE+CE≥AC(当且仅当点E′、点E在AC上时,取等号),
∴AE+BE+CE有最小值,最小值为A′C的长,设正方形的边长为a,
在Rt△A′BH中,∠A′BH=30°,
∴A′H=
A′B=
a,BH=
A′H=
a,
∴CH=a+
a,
在Rt△A′CH中,A′C2=A′H2+CH2,
∴(
a)2+(a+
a)2=(
+
)2,
解得a=2.
∴正方形的边长为2.

∵BE=BE′,∠EBE′=90°,AE=CE′,
∴EE′=
| 2 |
∵EA2+EC2=2EB2,
∴CE′2+EC2=EE′2,
∴∠ECE′=90°,
∴∠ECB+∠BCE′=∠ECB+∠BAE=90°,
∴A、E、C共线,
∴点E在正方形ABCD的对角线上.
(2) 如图2中,将△ABE绕点B逆时针旋转60°得△A′BE′,连结A′C,作A′H⊥BC于H.

∵△ABE绕点B逆时针旋转60°得△A′BE′,
∴BE=BE′,∠EBE′=60°,
∴△EBE′为等边三角形,
∴EE′=BE,
∴A′E′=AE,BA′=BA=2,∠ABA′=60°,
∵A′E′+E′E+EC≥A′C,
∴AE+BE+CE≥AC(当且仅当点E′、点E在AC上时,取等号),
∴AE+BE+CE有最小值,最小值为A′C的长,设正方形的边长为a,
在Rt△A′BH中,∠A′BH=30°,
∴A′H=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴CH=a+
| ||
| 2 |
在Rt△A′CH中,A′C2=A′H2+CH2,
∴(
| 1 |
| 2 |
| ||
| 2 |
| 6 |
| 2 |
解得a=2.
∴正方形的边长为2.
看了 已知:正方形ABCD内一点E...的网友还看了以下:
张边长是(20倍根号3-6倍根号2)cm的正方形硬纸,在四角均截去边长为2倍根号2cm的小正方形, 2020-04-25 …
一个棱长为0.2米的正方体纸箱(1)计算它的体积为多少立方米?(2)如果用边长为2×10的负2次方 2020-05-14 …
1):长方体水箱长0.8米,宽0.6米,深0.9米,装满水后倒入棱长1.2米的正方体水箱内,求水深 2020-05-16 …
用直尺和圆规完成以下问题(保留作图痕迹,不必写作法)(1)请在图(1)的正方形ABCD内,画出使∠ 2020-05-16 …
IMO2009中的高等数学符号问题,n是一个正整数,设a[1],a[2],...,a[k](k≥2 2020-06-02 …
有一个花坛,高0.5米底面是边长1.2米的正方形,四周用砖砌成厚度为0.3米这个花坛占地多少平方米 2020-06-19 …
1.有一块陵长是80厘米的正方体的铁块,现在要把它溶成一个横截面积是20平方厘米的正方体,这个长方 2020-06-25 …
在单位圆中,画π∕6,2π∕3的正玄线和余弦线,并求出这两个角的终边与单位圆的交点坐标,以及角π∕ 2020-07-02 …
小张将边长为a(a>2)米的正方形木板去掉一个边长为2米的正方形后余下的部分刷上油漆,小李将一个边 2020-07-11 …
代数式2(y-2)的正确含义是()A.2乘以y减2B.2与y的积减去2C.y与2的差的2倍D.y的 2020-07-21 …