早教吧作业答案频道 -->数学-->
问题情境:在学完2.4节圆周角之后,老师出了这样一道题:如图1,已知点A为∠MPN的平分线PQ上的任一点,以AP为弦作圆O与边PM、PN分别交于B、C两点,连结AB、BC、CA,形成了圆O的内接△ABC.
题目详情
问题情境:在学完2.4节圆周角之后,老师出了这样一道题:
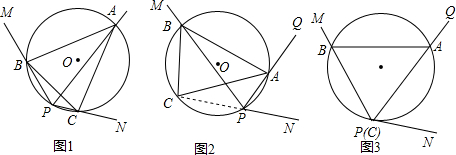
如图1,已知点A为∠MPN的平分线PQ上的任一点,以AP为弦作圆O与边PM、PN分别交于B、C两点,连结AB、BC、CA,形成了圆O的内接△ABC.小明同学发现△ABC是一个等腰三角形,理由是∠ABC=∠APC,∠ACB=∠APB,又由角平分线得∠APC=∠APB,所以∠ABC=∠ACB,AB=AC得证.
请你说出小明使用的是圆周角的哪个性质:___(只写文字内容).
深入探究:爱钻研的小慧却画出了图2,与边PN的反向延长线交于点C,其它条件不变,△ABC仍是等腰三角形,请你写出证明过程.
拓展提高:妙想的小聪提出如图3,如果圆O与边PN相切于点C(与P点已重合),其它条件不变,△ABC仍是等腰三角形吗?若是,请写出证明过程;若不是,请说明理由.
如图1,已知点A为∠MPN的平分线PQ上的任一点,以AP为弦作圆O与边PM、PN分别交于B、C两点,连结AB、BC、CA,形成了圆O的内接△ABC.小明同学发现△ABC是一个等腰三角形,理由是∠ABC=∠APC,∠ACB=∠APB,又由角平分线得∠APC=∠APB,所以∠ABC=∠ACB,AB=AC得证.
请你说出小明使用的是圆周角的哪个性质:___(只写文字内容).
深入探究:爱钻研的小慧却画出了图2,与边PN的反向延长线交于点C,其它条件不变,△ABC仍是等腰三角形,请你写出证明过程.
拓展提高:妙想的小聪提出如图3,如果圆O与边PN相切于点C(与P点已重合),其它条件不变,△ABC仍是等腰三角形吗?若是,请写出证明过程;若不是,请说明理由.

▼优质解答
答案和解析
问题情境:同弧所对的圆周角相等,
深入探究:△ABC仍是等腰三角形,理由如下:
∵∠ABC+∠APC=180°,∠APN+∠APC=180°,
∴∠ABC=∠APN.
∵PA 平分∠MPN,
∴∠APB=∠APN,
∴∠ABC=∠APB.
而∠APB=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
拓展提高:△ABC仍是等腰三角形理由如下:
作直径CH,连结AH,
∵CH为直径,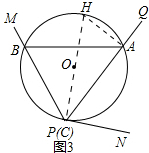
∴∠AHC=90°,
∴∠H+∠ACH=90°.
∵CN与圆O相切,
∴CN⊥CH,
∴∠ACN+∠ACH=90°,
∴∠ACN=∠H.
∵∠ABC=∠H,
∴∠ACN=∠ABC.
∵PA 平分∠MPN,
∴∠ACB=∠CAN.
∴∠ABC=∠ACB,
∴AB=AC.
深入探究:△ABC仍是等腰三角形,理由如下:
∵∠ABC+∠APC=180°,∠APN+∠APC=180°,
∴∠ABC=∠APN.
∵PA 平分∠MPN,
∴∠APB=∠APN,
∴∠ABC=∠APB.
而∠APB=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
拓展提高:△ABC仍是等腰三角形理由如下:
作直径CH,连结AH,
∵CH为直径,

∴∠AHC=90°,
∴∠H+∠ACH=90°.
∵CN与圆O相切,
∴CN⊥CH,
∴∠ACN+∠ACH=90°,
∴∠ACN=∠H.
∵∠ABC=∠H,
∴∠ACN=∠ABC.
∵PA 平分∠MPN,
∴∠ACB=∠CAN.
∴∠ABC=∠ACB,
∴AB=AC.
看了 问题情境:在学完2.4节圆周...的网友还看了以下:
化学中能量变化量有正负吗?比如,A生成B,能量变化量20kj,那可以说这个反应吸热?那也就是说,我 2020-04-25 …
文件保密传递常常是按一定规则将其加密,收件人再按约定的规则将其解密,某电文按下面规则加密:将一个英 2020-05-13 …
文件保密传递常常是按一定规则将其加密,收件人再按约定的规则将其解密.某电文按下面规则加密:将一个英 2020-05-15 …
文件保密传递常常是按一定规则将其加密,收件人再按约定的规则将其解密,某电文按下面规则加密:将一个英 2020-05-17 …
文件保密传递常常是按一定规则将其加密,收件人再按约定的规则将其解密,某电文按下面规则加密:将一个英 2020-05-17 …
两个同样大小的长方体正好可以拼成一个正方体,如果拼成的正方体的棱长为a,每个长方体表面积是()两个 2020-06-04 …
下面这些题怎么写?都把我弄糊涂了,最好写出怎样判断、分析?题如下:如果Y=8X,X和Y()比例.A 2020-06-12 …
令a、b、c是互不相等的正数如何证明aˆ2+1/aˆ2≥a+1/a成立令a、b、c是互不相等的正数 2020-07-09 …
对于有理数a、b,|a+b|=|a|+|b|一定成立吗?如果成立,请说明理由;如果不成立,请问在什 2020-07-31 …
关于必要条件的问题如果B成立,那么A成立,即B→A,如果A不成立,那么B就一定不成立,即┐A→┐B, 2020-12-31 …