早教吧作业答案频道 -->数学-->
两个同心圆,PA切小圆于点A,PB切大圆于B,PA=3cm,PB=2cm,则两圆所围成的圆环面积是()A、1cm2B、5cm2C、πcm2D、5πcm2
题目详情
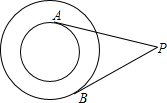 两个同心圆,PA切小圆于点A,PB切大圆于B,PA=3cm,PB=2cm,则两圆所围成的圆环面积是( )
两个同心圆,PA切小圆于点A,PB切大圆于B,PA=3cm,PB=2cm,则两圆所围成的圆环面积是( )| A、1cm 2 |
| B、5cm 2 |
| C、πcm 2 |
| D、5πcm 2 |
▼优质解答
答案和解析
考点:
切线的性质
专题:
分析:
连接OP、OA、OB,设OA=r,OB=R,求出圆环的面积是πR 2 -πr 2 =π(R 2 -r 2 ),由切线性质得出∠OAP=∠OBP=90°,由勾股定理得出OP 2 =OA 2 +PA 2 =OB 2 +PB 2 ,求出R 2 -r 2 =5,代入求出即可.
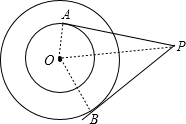
连接OP、OA、OB,设OA=r,OB=R,
则圆环的面积是πR 2 -πr 2 =π(R 2 -r 2 ),
∵两个同心圆,PA切小圆于点A,PB切大圆于B,
∴∠OAP=∠OBP=90°,
由勾股定理得:OP 2 =OA 2 +PA 2 =OB 2 +PB 2 ,
∴3 2 +r 2 =R 2 +2 2 ,
∴R 2 -r 2 =5,
∴圆环的面积是πR 2 -πr 2 =π(R 2 -r 2 )=5π(cm 2 ),
故选D.
点评:
本题考查了切线的性质,勾股定理的应用,关键是得出圆环的面积是πR 2 -πr 2 =π(R 2 -r 2 )和求出R 2 -r 2 的值.
考点:
切线的性质
专题:
分析:
连接OP、OA、OB,设OA=r,OB=R,求出圆环的面积是πR 2 -πr 2 =π(R 2 -r 2 ),由切线性质得出∠OAP=∠OBP=90°,由勾股定理得出OP 2 =OA 2 +PA 2 =OB 2 +PB 2 ,求出R 2 -r 2 =5,代入求出即可.

连接OP、OA、OB,设OA=r,OB=R,
则圆环的面积是πR 2 -πr 2 =π(R 2 -r 2 ),
∵两个同心圆,PA切小圆于点A,PB切大圆于B,
∴∠OAP=∠OBP=90°,
由勾股定理得:OP 2 =OA 2 +PA 2 =OB 2 +PB 2 ,
∴3 2 +r 2 =R 2 +2 2 ,
∴R 2 -r 2 =5,
∴圆环的面积是πR 2 -πr 2 =π(R 2 -r 2 )=5π(cm 2 ),
故选D.
点评:
本题考查了切线的性质,勾股定理的应用,关键是得出圆环的面积是πR 2 -πr 2 =π(R 2 -r 2 )和求出R 2 -r 2 的值.
看了 两个同心圆,PA切小圆于点A...的网友还看了以下:
关于百分比的平均数算法(2/2+2/4)/2与(2+2)/(2+4)有区别吗无敌变种版问题:2个苹果 2020-03-30 …
用化学符号表示.2个氦原子3个碘分子4个硫酸根离子+5价的磷元素4个氯化氢分子2个氧原子1个钾原子3 2020-03-30 …
预习数学的时产生了疑惑.2的负2次方等于多少?(一下个人理解)2³=2×2×2=8(表示为3个2相 2020-05-21 …
有5个筛子,求下面这几种情况的概率.答案要是几分之几这种的,不要什么c多少多少的那种.5个1--- 2020-06-12 …
(2009•锦州)如图所示,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上 2020-06-13 …
如干个1与2排成一行:1,2,1,2,2,1,2,2,2,1,2……规则是:第一个数是1,第2个数是 2020-11-06 …
任意写出一个2位数,交换这个2位数的十位数字和个位数字,得带一个新的2位数,(1)求这2个2位数的和 2020-11-18 …
若干个1与2排成1行:1,2,1,2,2,1,2,2,2,1,2……,规则是:第1个数是1,第2个数 2020-11-18 …
一堆苹果,2个2个地数剩1个,3个3个地数剩2个,4个4个地数剩3个,5个5个地数剩4个,6个6个地 2020-11-19 …
扑克牌智力题如下甲方:1个2,3个K,3个Q,2个9,2个7,2个6,2个5,2个4,1个3乙方:2 2020-11-28 …