早教吧作业答案频道 -->数学-->
(1)问题发现:如图1,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.填空:①四边形AFMG的形状是;
题目详情
(1)问题发现:
如图1,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.
填空:①四边形AFMG的形状是___;
②△DFM和△MGE之间的关系是___.
(2)拓展探究:
如图2,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°,点F、M、G分别为AB、BC、AC边的中点,试判断△DFM和⊥MGE之间的关系,并加以说明.
(3)问题解决:
在(2)的条件下,若AD=5,AB=6,△DFM的面积为32,直接写出△MGE的面积.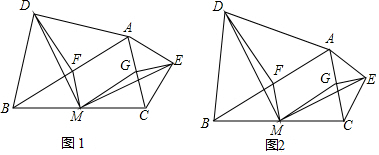
如图1,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.
填空:①四边形AFMG的形状是___;
②△DFM和△MGE之间的关系是___.
(2)拓展探究:
如图2,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°,点F、M、G分别为AB、BC、AC边的中点,试判断△DFM和⊥MGE之间的关系,并加以说明.
(3)问题解决:
在(2)的条件下,若AD=5,AB=6,△DFM的面积为32,直接写出△MGE的面积.

▼优质解答
答案和解析
(1)①∵BF=AF,BM=MC,
∴FM∥AC,同理MG∥AB,
∴四边形AFMG是平行四边形,
故答案为:平行四边形;
②∵∠BDA=90°,DF是AB边上的中线,
∴DF=AF.
∵四边形AFMG是平行四边形,
∴MG=AF,∠AFM=∠AGM.
∴DF=MG,∠BFM=∠MGC.
∵∠AEC=90°,EG是AC边上的中线,
∴GE=AG.
∵四边形AFMG是平行四边形,
∴AG=FM.
∴GE=FM.
∵DA=DB,F为AB的中点,
∴∠DFB=90°.
同理:∠EGC=90°.
∴∠DFB+∠BFM=∠EGC+∠MGC,即∠DFM=∠EGM.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS);
故答案为:△DFM≌△MGE.
(2)△DFM∽△MGE,理由如下:
∵△ADB和△ACE都是等腰三角形,且F、G为AB、AC的中点,
∴∠DFB=∠EGC=90°.
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=
AC=AG MG=
AB=AF.
∴∠BFM=∠BAC=∠MGC.
∴∠BFM+90°=∠MGC+90°,
即∠DFM=∠MGE.
∵∠BAD+∠CAE=90°,∠CAE+∠AEG=90°,
∴∠BAD=∠AEG.
∴tan∠BAD=tan∠AEG.
∴
=
,即
=
,
又∵∠DFM=∠MGE,
∴△DFM∽△MGE.
(3)∵AD=5,AB=6,
∴AF=3,MG=3,MG=AF=3.
∴在Rt△ADF中,DF=
=
=4.
∵由①知△DFM∽△MGE,且△DFM的面积为32,
∴
=(
)2=(
)2=
.
∴S△MGE=32×
=18.
∴FM∥AC,同理MG∥AB,
∴四边形AFMG是平行四边形,
故答案为:平行四边形;
②∵∠BDA=90°,DF是AB边上的中线,
∴DF=AF.
∵四边形AFMG是平行四边形,
∴MG=AF,∠AFM=∠AGM.
∴DF=MG,∠BFM=∠MGC.
∵∠AEC=90°,EG是AC边上的中线,
∴GE=AG.
∵四边形AFMG是平行四边形,
∴AG=FM.
∴GE=FM.
∵DA=DB,F为AB的中点,
∴∠DFB=90°.
同理:∠EGC=90°.
∴∠DFB+∠BFM=∠EGC+∠MGC,即∠DFM=∠EGM.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS);
故答案为:△DFM≌△MGE.
(2)△DFM∽△MGE,理由如下:
∵△ADB和△ACE都是等腰三角形,且F、G为AB、AC的中点,
∴∠DFB=∠EGC=90°.
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BFM=∠BAC=∠MGC.
∴∠BFM+90°=∠MGC+90°,
即∠DFM=∠MGE.
∵∠BAD+∠CAE=90°,∠CAE+∠AEG=90°,
∴∠BAD=∠AEG.
∴tan∠BAD=tan∠AEG.
∴
| DF |
| AF |
| AG |
| GE |
| DF |
| MG |
| FM |
| GE |
又∵∠DFM=∠MGE,
∴△DFM∽△MGE.
(3)∵AD=5,AB=6,
∴AF=3,MG=3,MG=AF=3.
∴在Rt△ADF中,DF=
| AD2-AF2 |
| 52-32 |
∵由①知△DFM∽△MGE,且△DFM的面积为32,
∴
| S△MGE |
| S△DFM |
| MG |
| DF |
| 3 |
| 4 |
| 9 |
| 16 |
∴S△MGE=32×
| 9 |
| 16 |
看了 (1)问题发现:如图1,在△...的网友还看了以下:
1/a+1/b+1/c=1/d+1/e+1/f+1/g=1(a,b,c,d,e,f,g均为自然数) 2020-05-13 …
设U为全集,子集A={x/f(x)=0},B={x/g(x)=0},C={x/h(x)=0},则方 2020-05-15 …
设栈的初始为空,元素a,b,c,d,e,f,g依次入栈,以下出栈序列不可能出现的是A,a,b,c, 2020-05-17 …
DNA碱基比的问题在DNA分子的双链结构中,下列何者的比例会因为生物种类而不同?A(A+U)/(G 2020-05-20 …
A.(B, F, G, J, A, E, D, I, C, H)B.(B, A, D, E, F, 2020-05-26 …
设f(x),g(x)在[a,b]上连续,且均为严格单增的正函数,证明:存在c€(a,b)使f(b) 2020-06-18 …
为什么a+b≠c+d体系中气体物质的总物质的量保持不变表明反应达到平衡状态对于纯气体反应aA(g) 2020-06-21 …
(A+B+C+D)^4=?(A+B+C+D+E)^5=?(A+B+C+D+E+F)^6=?(A+B 2020-07-18 …
如何证明积分中值定理的推论?重谢!设函数f和g在[a,b]上可积.若g为单调函数且在(a,b)上不 2020-07-30 …
求解多元一次不等式的编程47a-b-c-d-e-f-g>047b-a-c-d-e-f-g>023c- 2020-12-14 …