早教吧作业答案频道 -->数学-->
如图,边长为6的正方形ABCD中,点E是BC上一点,点F是AB上一点.点F关于直线DE的对称点G恰好在BC延长线上,FG交DE于点H.点M为AD的中点,若MH=17,则EG=.
题目详情
如图,边长为6的正方形ABCD中,点E是BC上一点,点F是AB上一点.点F关于直线DE的对称点G恰好在BC延长线上,FG交DE于点H.点M为AD的中点,若MH=
,则EG=___.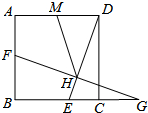
| | 17 |

▼优质解答
答案和解析
连接DF,DG,过H作HP⊥AB于P,HQ⊥AD于Q,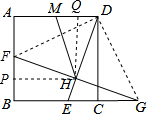
∵点F,点G关于直线DE的对称,
∴DF=DG,
正方形ABCD中,∵AD=CD,∠ADC=∠A=∠BCD=90°,
∴∠GCD=90°,又在Rt△AFD与Rt△CDG中,
,
∴Rt△AFD≌Rt△CDG,
∴∠ADF=∠CDG,
∴∠FDG=∠ADC=90°,
∴△FDG是等腰直角三角形,
∵DH⊥CF,
∴DH=FH=
FG,
∵HP⊥AB,HQ⊥AD,∠A=90°,
∴四边形APHQ是矩形,
∴∠PHQ=90°,
∵∠DHF=90°,
∴∠PHF=∠DHQ,又在△PFF与△DQH中有
,
∴△HPF≌△DHQ,
∴HP=HQ,所以矩形APHQ是正方形;
设正方形APHQ边长为a,则在Rt△MQH中,有(a-3)2+a2=17,解得a=4;
∴FP=QD=AD-AQ=6-4=2,
又易证△FPH∽△EHG,则有
=
,即EG=
,
又FH2=22+42=20,PH=4,
∴EG=5
故答案为:5.

∵点F,点G关于直线DE的对称,
∴DF=DG,
正方形ABCD中,∵AD=CD,∠ADC=∠A=∠BCD=90°,
∴∠GCD=90°,又在Rt△AFD与Rt△CDG中,
|
∴Rt△AFD≌Rt△CDG,
∴∠ADF=∠CDG,
∴∠FDG=∠ADC=90°,
∴△FDG是等腰直角三角形,
∵DH⊥CF,
∴DH=FH=
| 1 |
| 2 |
∵HP⊥AB,HQ⊥AD,∠A=90°,
∴四边形APHQ是矩形,
∴∠PHQ=90°,
∵∠DHF=90°,
∴∠PHF=∠DHQ,又在△PFF与△DQH中有
|
∴△HPF≌△DHQ,
∴HP=HQ,所以矩形APHQ是正方形;
设正方形APHQ边长为a,则在Rt△MQH中,有(a-3)2+a2=17,解得a=4;
∴FP=QD=AD-AQ=6-4=2,
又易证△FPH∽△EHG,则有
| EG |
| FH |
| GH |
| PH |
| FH2 |
| PH |
又FH2=22+42=20,PH=4,
∴EG=5
故答案为:5.
看了 如图,边长为6的正方形ABC...的网友还看了以下:
已知可逆反应M(g)+N(g)=P(g)+Q(g)若其浓度为C(M)=1molC(N)=2.4mo 2020-04-11 …
已知可逆反应:M(g)+N(g)===(可逆符号)P(g)+Q(g);△H>0.(为?.已知可逆反 2020-04-27 …
溶解平衡的化学题对于难溶盐MR,其饱和溶液中M+和R-物质的量浓度也存在下列关系C(M+)*C(R 2020-05-22 …
层次模型不能直接表示( )A.1:1关系B.1:m关系C.m:n关系D.1:1和l:m关系 2020-05-23 …
幂函数g(x)=(m^2-m-1)x^m的图像关于y轴对称,且函数f(x)=g(x)-2ax+1在 2020-06-02 …
有A、B、C、D、E、F、G7种化合物和单质M,它们存在下列关系:①A+B=C↑+D②C(浓溶液) 2020-06-06 …
是关于c(m,n)和A(m,我记得这两个都是排律组合求概率用的c(m,n)是求n个数字里挑选m个数 2020-06-12 …
关于G=mg,下列说法正确的是()A.它表示G与m成正比B.它表示G与g成正比C.它表示g与m成反比 2020-10-30 …
浮力小问题,急!当物体漂浮时,F浮=G物,也可运用阿基米德原理F浮=G排这两个公式展开:F浮=G物= 2020-11-03 …
已知甲DNA分子的一条链中(A+G)/(T+C)=m,乙DNA分子的一条单链中(A+T)/(G+C) 2020-12-01 …