已知平面ABC外一点P，且PH⊥平面ABC于点H．给出下列四个命题：①若PA⊥BC，PB⊥AC，则点H是△ABC的垂心；②若PA，PB，PC两两互相垂直，则点H是△ABC的垂心；③若∠ABC=90°，点H是AC的中点，则P

Question

已知平面ABC外一点P，且PH⊥平面ABC于点H．给出下列四个命题：
①若PA⊥BC，PB⊥AC，则点H是△ABC的垂心；
②若PA，PB，PC两两互相垂直，则点H是△ABC的垂心；
③若∠ABC=90°，点H是AC的中点，则PA=PB=PC；
 ④若PA=PB=PC，则点H是△ABC的外心．
其中正确命题的个数为（　　）

A. 4

B. 3

C. 2

D. 1

Answer 1

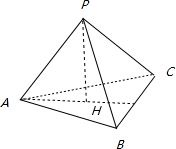∵PH⊥平面ABC，H为垂足．
∴PH⊥AB，PH⊥AC，PH⊥BC，
①若PA⊥BC，则BC⊥平面PAH，
∴BC⊥AH，同理：AC⊥BH，
则点H是△ABC的垂心，正确；
②若PA，PB，PC两两互相垂直，容易推出AH⊥BC，同理BH⊥AC，可得H是△ABC的垂心，正确．
③若∠ABC=90°，H是AC的中点，容易推出△PHA≌△PHB≌△PHC，则PA=PB=PC；正确．
④若PA=PB=PC，易得AH=BH=CH，则H是△ABC的外心，正确．
故正确的命题为：①②③④，
故选：A