早教吧作业答案频道 -->数学-->
已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形过点F作BC的平行线交射线AC于点E,连接BF(1)如图1,若△ABC的边长是2,求△ADF的最小面积;(
题目详情
已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形过点F作BC的平行线交射线AC于点E,连接BF
(1)如图1,若△ABC的边长是2,求△ADF的最小面积;
(2)如图1,求证:△AFB≌△ADC';
(3)如图2,若D点在BC边的延长线上,其它条件不变,请判断四边形BCEF的形状,并说明理由.
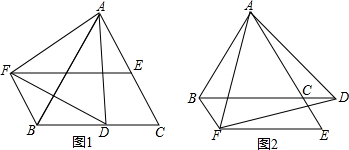
(1)如图1,若△ABC的边长是2,求△ADF的最小面积;
(2)如图1,求证:△AFB≌△ADC';
(3)如图2,若D点在BC边的延长线上,其它条件不变,请判断四边形BCEF的形状,并说明理由.

▼优质解答
答案和解析
(1)由题意得当AD⊥BC时,AD最小,即△ADF的面积最小,
∵△ABC是等边三角形,
∴BC=2,BD=CD=1,
∴AD=
,
∵△ADF是等边三角形,
∴△ADF的最小面积=
;
(2)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
(3)∵△ABC和△ADE都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
,
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
∵△ABC是等边三角形,
∴BC=2,BD=CD=1,
∴AD=
| 3 |
∵△ADF是等边三角形,
∴△ADF的最小面积=
3
| ||
| 4 |
(2)∵△ABC和△ADF都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
|
∴△AFB≌△ADC(SAS);
(3)∵△ABC和△ADE都是等边三角形,
∴AF=AD,AB=AC,∠FAD=∠BAC=60°,
又∵∠FAB=∠FAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠FAB=∠DAC,
在△AFB和△ADC中,
|
∴△AFB≌△ADC(SAS);
∴∠AFB=∠ADC.
又∵∠ADC+∠DAC=60°,∠EAF+∠DAC=60°,
∴∠ADC=∠EAF,
∴∠AFB=∠EAF,
∴BF∥AE,
又∵BC∥EF,
∴四边形BCEF是平行四边形.
看了 已知△ABC是等边三角形,D...的网友还看了以下:
可逆反应3A(g)⇌3B(?)+C(?)(正反应吸热),随着温度的升高,气体相对分子质量变小,则下 2020-05-12 …
已知A、B、C三点不共线,对平面ABC外的任一点O,确定在下列条件下,点M是否与A、B、C一定共面 2020-05-13 …
物块C上放着物块A和B,水平力F作用于A,使A、B、C一起做匀速运动,各接触面间的摩擦力情况是a 2020-05-16 …
在()中,a和b成正比例c/a=b(c一定,a不等于0)ab=c(c一定,a,b不为0)a/b=c 2020-06-14 …
下列句子没有语病的一项是()A.在纪念李谷一从艺五十周年的文艺晚会上,文化界知名人士们声情并茂地演 2020-07-08 …
如图,已知圆心为A,B,C的三个圆彼此相切,且均与直线l相切.若⊙A,⊙B,⊙C的半径分别为a,b 2020-07-31 …
a、b和c是三个自然数(且不等于0),在a=b×c中A、b一定是a的约数B、c一定是a和b的最大公 2020-07-31 …
若向量a不等于0,b=a/(a),c=(cosθ,sinθ),则b与c一定满足A.b=cB.b*c 2020-08-01 …
如图,CD垂直于AB于D,且有AC^2=AD*AB.求证;1)CD^2=AD*BD2)三角形ACB为 2020-11-01 …
下面的判断是否正确?请说明理由.(1)如果a>b,b≥c,那么a≥c(2)已知线段AB=5cm,线段 2020-11-02 …