早教吧作业答案频道 -->数学-->
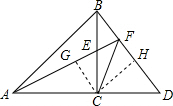
如图,CA=CB,E在BC上,且CE=CD,∠ACB=∠DCE=90°,AE的延长线交BD于F,连接CF.(1)求证:AE=BD;(2)求证:CF平分∠AFD.
题目详情
如图,CA=CB,E在BC上,且CE=CD,∠ACB=∠DCE=90°,AE的延长线交BD于F,连接CF.

(1)求证:AE=BD;
(2)求证:CF平分∠AFD.

(1)求证:AE=BD;
(2)求证:CF平分∠AFD.
▼优质解答
答案和解析
 (1)证明:在△ACE与△BCD中,
(1)证明:在△ACE与△BCD中,
∵
,
∴△ACE≌△BCD,
∴AE=BD;
(2)证明:过点C作CG⊥AF,CH⊥BD,垂足分别为G、H,
∵由(1)知,△ACE≌△BCD,
∴∠CAG=∠CBH,AC=BC.
在△ACG与△BCH中,
∵
,
∴△ACG≌△BCH(AAS),
∴CG=CH,
∴CF平分∠AFD.
 (1)证明:在△ACE与△BCD中,
(1)证明:在△ACE与△BCD中,∵
|
∴△ACE≌△BCD,
∴AE=BD;
(2)证明:过点C作CG⊥AF,CH⊥BD,垂足分别为G、H,
∵由(1)知,△ACE≌△BCD,
∴∠CAG=∠CBH,AC=BC.
在△ACG与△BCH中,
∵
|
∴△ACG≌△BCH(AAS),
∴CG=CH,
∴CF平分∠AFD.
看了 如图,CA=CB,E在BC上...的网友还看了以下:
满足{a}⊆M⊆{a,b,c,d}的集合M的个数是( ) 是{a} {a,b} {a,c} {a, 2020-04-05 …
已知a/b=c/d=e/f=2,当b+d≠0时,a+c/b+d=;当b+d+f≠0时,a+c+e/ 2020-05-14 …
若非空集合M⊆N={a,b,c,d},则M的个数为8个{a},{b},{c},{d},{a,b}, 2020-05-15 …
在Excel中可选取( )单元格。 A.单个 B.多个 C.连续 D.不连续 2020-05-19 …
滑动变阻器的连接?滑片P往左(A,B和C,D和A,C和A,D和B,C和B,D)请一一告诉我他们哪些 2020-05-20 …
在关系代数的连接操作中,( )操作需要取消重复列。A)等值连接 B)自然连接 C)θ连接 D)笛 2020-05-23 …
在关系代数的连接操作中,( )操作需要取消重复列。A)等值连接B)自然连接C)θ连接D)笛卡儿积 2020-05-24 …
UDP提供面向______的传输服务。A.端B.地址C.连接D.无连接 2020-05-26 …
对于任意的两个实数对(a,b)和(c,d),规定:当a=c,b=d时,有(a,b)=(c,d);运 2020-07-06 …
已知a,b,c,d都是常数,a>b,c>d,若f(x)=2017-(x-a)(x-b)的零点为c, 2020-07-20 …