给出定理:若函数f(x)在闭区间[a,b]上连续,且在开区间(a,b)内可导,则在区间(a,b)内至少存在一点x=ξ,使得f(a)-f(b)=f′(ξ)(a-b)成立.根据这一
给出定理:若函数 f ( x )在闭区间[ a , b ]上连续,且在开区间( a , b )内可导,则在区间( a , b )内至少存在一点 x = ξ ,使得 f ( a )- f ( b )= f ′( ξ )( a - b )成立.
根据这一定理判断:
若 x 1 , x 2 是相应函数定义域内的任意两点,则下列给出的四个函数中使得不等式| f ( x 1 )- f ( x 2 )|≤| x 1 - x 2 |恒成立的是________(写出你认为所有符合条件的函数的序号).
① f ( x )=sin x ② f ( x )= x +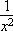
③ f ( x )=ln( x 2 +1) ④ f ( x )= x e x
已知:f(x)=lg(a^x-b^x)(a>1>b>0)若f(x)在(1,+∞)内恒为正,试比较a 2020-05-13 …
已知函数f(x)=2(根号3)sin(x/3)cos(x/3)-2sin²(x/3)(1)若x∈【 2020-05-16 …
已知函数f(x)=1-cosx+sin(x+π/6) 1求f(x)的最小正周期,2,记△ABC的内 2020-05-16 …
已知向量m=[2cos(x/2),1],n=[sin(x/2),1](x属于R),设函数f(x)= 2020-05-17 …
设f(x)为偶函数,且在[0,+无穷大)内是增函数,又f(-3)=0,则x•f(x)<0的解集.已 2020-05-21 …
以下四个命题中,正确的是()A.若f′(x)在(0,1)内连续,则f(x)在(0,1)内有界B.若 2020-06-23 …
若函数y=f(x)满足f(-x)=f(x),当a,b∈(-∞,0]时总有f(a)−f(b)a−b> 2020-06-27 …
函数f(x)=Asin(2x+φ)(|φ|≤π2,A>0)部分图象如图所示,且f(a)=f(b)= 2020-07-26 …
对定义在[1,+∞)上的函数f(x)和常数a,b,若f(2x)=af(x)+b恒成立,则称(a,b 2020-07-30 …
已知函数f(x)=sin(2x+π/3)+sin(2x-π/3)+根号3*cos2x-m,若f(x) 2020-11-01 …