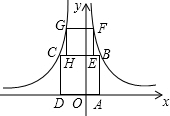
如图，四边形ABCD与EFGH均为正方形，点B、F在函数y=1x（x>0）的图象上，点G、C在函数y=-3x（x<0）的图象上，点A、D在x轴上，点H、E在线段BC上，则点G

Question

如图，四边形ABCD与EFGH均为正方形，点B、F在函数y= (1)/(x)（x>0）的图象上，点G、C在函数y=- (3)/(x)（x<0）的图象上，点A、D在x轴上，点H、E在线段BC上，则点G的纵坐标___．

Answer 1

设线段AB的长度为a，线段EF的长度为b（a>0，b>0），
令y=(1)/(x)（x>0）中y=a，则x=(1)/(a)，
即点B的坐标为（(1)/(a)，a）；
令y=-(3)/(x)（x<0）中y=a，则x=-(3)/(a)，
即点C的坐标为（-(3)/(a)，a）．
∵四边形ABCD为正方形，
∴(1)/(a)-（-(3)/(a)）=a，
解得：a=2，或a=-2（舍去）．
令y=(1)/(x)（x>0）中y=2+b，则x=(1)/(2+b)，
即点F的坐标为（(1)/(2+b)，2+b）；
令y=-(3)/(x)（x<0）中y=2+b，则x=-(3)/(2+b)，
即点G的坐标为（-(3)/(2+b)，2+b）．
∵四边形EFGH为正方形，
∴(1)/(2+b)+（-(3)/(2+b)）=b，即b²+2b-4=0，
解得：b=√(5)-1，或b=-√(5)-1（舍去）．
∴a+b=2+√(5)-1=√(5)+1．
故答案为：√(5)+1．