早教吧作业答案频道 -->数学-->
已知关于x的方程kx2+(2k+1)x+2=0.(1)求证:无论k取任何实数时,方程总有实数根;(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1
题目详情
已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
▼优质解答
答案和解析
(1)证明:①当k=0时,方程为x+2=0,所以x=-2,方程有实数根,
②当k≠0时,∵△=(2k+1)2-4k×2=(2k-1)2≥0,即△≥0,
∴无论k取任何实数时,方程总有实数根;
(2) 令y=0,则kx2+(2k+1)x+2=0,
解关于x的一元二次方程,得x1=-2,x2=-
,
∵二次函数的图象与x轴两个交点的横坐标均为整数,且k为正整数,
∴k=1.
∴该抛物线解析式为y=x2+3x+2,
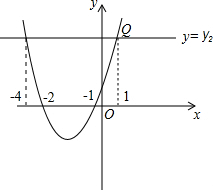
由图象得到:当y1>y2时,a>1或a<-4.
(3)依题意得kx2+(2k+1)x+2-y=0恒成立,即k(x2+2x)+x-y+2=0恒成立,
则
,
解得
或
.
所以该抛物线恒过定点(0,2)、(-2,0).
②当k≠0时,∵△=(2k+1)2-4k×2=(2k-1)2≥0,即△≥0,
∴无论k取任何实数时,方程总有实数根;
(2) 令y=0,则kx2+(2k+1)x+2=0,
解关于x的一元二次方程,得x1=-2,x2=-
| 1 |
| k |
∵二次函数的图象与x轴两个交点的横坐标均为整数,且k为正整数,
∴k=1.
∴该抛物线解析式为y=x2+3x+2,

由图象得到:当y1>y2时,a>1或a<-4.
(3)依题意得kx2+(2k+1)x+2-y=0恒成立,即k(x2+2x)+x-y+2=0恒成立,
则
|
解得
|
|
所以该抛物线恒过定点(0,2)、(-2,0).
看了 已知关于x的方程kx2+(2...的网友还看了以下:
已知抛物线y=x^2;+bx+c经过点(1,-5)和(-2,4)(1)求这条抛物线的解析式(2)设 2020-05-20 …
(2014•株洲)已知抛物线y=x2-(k+2)x+5k+24和直线y=(k+1)x+(k+1)2 2020-06-12 …
下列不属于动物交流信息的是()A.母鸡召唤小鸡B.蜜蜂的舞蹈C.狼群的嚎叫D.苍蝇飞行时的嗡嗡声 2020-07-01 …
已知抛物线y=-(4/9)x^2+bx+c与X轴相交于A.B两点,其对称轴为直线x=2,且与x轴相 2020-08-01 …
设集合A={X|-2小于X小于-1}并{X|X大于1},B={X|a小于等于X小于等于b},若A并 2020-08-02 …
下列不属于动物交流信息的是()A.公鸡找到食物后发出“咯咯”的叫声B.雌性萤火虫尾端发出闪闪荧光C. 2020-11-02 …
1.物物交换有利于促进商品流通2.物物交换是商品流通1.物物交换有利于促进商品流通2.物物交换是商品 2020-12-05 …
设点(x1,y1)在圆C:x^2+y^2=1的内部,则直线x1x+y1y=1和圆a、不相交b、有两个 2020-12-28 …
一元二次不等式求不等式M-1大于或等于-2与M(M-1)小于或等于2的交集(两式的等于不能同时取得) 2021-02-04 …
A={x|-2小于x小于1或x大于1},B={a小于等于x小于等于b},A并B={x|x大于-2}, 2021-02-05 …