早教吧作业答案频道 -->数学-->
我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是时
题目详情
我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是___时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是___时,它们一定不全等.
▼优质解答
答案和解析
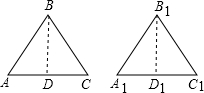 已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,
则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,
在△BDC和△B1D1C1中,
,
∴△BDC≌△B1D1C1,
∴BD=B1D1,
在Rt△BDA和Rt△B1D1A1中
,
∴Rt△BDA≌Rt△B1D1A1(HL),
∴∠A=∠A1,
在△ABC和△A1B1C1中
,
∴△ABC≌△A1B1C1(AAS).
同理可得:当这两个三角形都是钝角三角形或直角三角形时,它们也会全等,
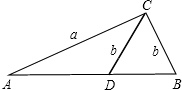
如图:△ACD与△ACB中,
CD=CB,AC=AC,∠A=∠A,
但:△ACD与△ACB不全等.
 ,
,
故当这两个三角形其中一个三角形是锐角三角形,另一个是钝角三角形时,它们一定不全等.
故答案为:钝角三角形或直角三角形,钝角三角形.
 已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.求证:△ABC≌△A1B1C1.
证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,
则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,
在△BDC和△B1D1C1中,
|
∴△BDC≌△B1D1C1,
∴BD=B1D1,
在Rt△BDA和Rt△B1D1A1中
|
∴Rt△BDA≌Rt△B1D1A1(HL),
∴∠A=∠A1,
在△ABC和△A1B1C1中
|
∴△ABC≌△A1B1C1(AAS).
同理可得:当这两个三角形都是钝角三角形或直角三角形时,它们也会全等,
如图:△ACD与△ACB中,
CD=CB,AC=AC,∠A=∠A,
但:△ACD与△ACB不全等.
 ,
,故当这两个三角形其中一个三角形是锐角三角形,另一个是钝角三角形时,它们一定不全等.
故答案为:钝角三角形或直角三角形,钝角三角形.
看了 我们知道:“两边及其中一边的...的网友还看了以下:
如何解释下面判断全等三角形的条件?设有两边和一角对应相等的两个三角形,则①若这个角的对边恰为这两边 2020-04-26 …
已知椭圆C:y^/a^2+x^2/b^2=1(a>b>0)的焦点和上顶点分别为F1F2B我们称三角 2020-06-03 …
芳芳和圆圆一起玩用火柴棍摆图形的游戏.他们摆三角形和正方形一共用了26根火柴棍(任意两个图形之间没 2020-06-27 …
11.下列四组中一定是全等三角形的为()A.三内角分别相等的两三角形B.斜边相等的两直角三角形C. 2020-08-01 …
下列命题中正确的个数是()①全等三角形对应边相等;②三个角对应相等的两个三角形全等;③三边对应相等 2020-08-01 …
初中数学~证明三角形相似的相关定理~91、相似三角形判定定理1两角对应相等,两三角形相似(ASA) 2020-08-01 …
下列命题错误的是()A.两边和其中一边上的中线对应相等的两个三角形全等B.两边和第三边上的中线对应 2020-08-01 …
将下列各命题的题设和结论互相颠倒,继而可将它们分别变成否定式,得到新的命题,并判断这些命题的真假.( 2020-11-01 …
(2013•沈阳)定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质:如果两个三角 2020-11-04 …
定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质:如果两个三角形是“友好三角形” 2020-11-04 …