早教吧作业答案频道 -->数学-->
如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点.(1)求异面直线B1O与AM所成角的大小.(2)求二面角B1-MA-C的正切值.
题目详情
如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点.
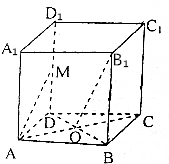
(1)求异面直线B1O与AM所成角的大小.
(2)求二面角B1-MA-C的正切值.

(1)求异面直线B1O与AM所成角的大小.
(2)求二面角B1-MA-C的正切值.
▼优质解答
答案和解析
 (1)∵BB1⊥平面ABCD,OB⊥AC,
(1)∵BB1⊥平面ABCD,OB⊥AC,
∴B1O⊥AC.设棱长为2
连接MO、MB1,则MO=
,B1O=
,MB1=3.
∵MO2+B1O2=MB12,∴∠MOB1=90°.
∴B1O⊥MO.
∵MO∩AC=O,∴B1O⊥平面MAC.
∴B1O⊥AM,
∴异面直线B1O与AM所成角为90°;
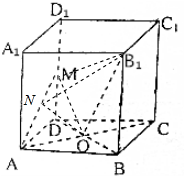
(2)作ON⊥AM于点N,连接B1N.
∵B1O⊥平面MAC,∴AM⊥平面B1ON.
∴B1N⊥AM.
∴∠B1NO就是二面角B1-MA-C的平面角.
∵AM=
,CM=
,∴AM=CM.
又O为AC的中点,∴OM⊥AC.则ON=OAsin∠MAO=
.
在Rt△B1ON中,tan∠B1NO=
=
,
∴∠B1NO=arctan
,即所求二面角的大小为arctan
.
 (1)∵BB1⊥平面ABCD,OB⊥AC,
(1)∵BB1⊥平面ABCD,OB⊥AC,∴B1O⊥AC.设棱长为2
连接MO、MB1,则MO=
| 3 |
| 6 |
∵MO2+B1O2=MB12,∴∠MOB1=90°.
∴B1O⊥MO.
∵MO∩AC=O,∴B1O⊥平面MAC.
∴B1O⊥AM,
∴异面直线B1O与AM所成角为90°;
(2)作ON⊥AM于点N,连接B1N.
∵B1O⊥平面MAC,∴AM⊥平面B1ON.
∴B1N⊥AM.
∴∠B1NO就是二面角B1-MA-C的平面角.
∵AM=
| 5 |
| 5 |
又O为AC的中点,∴OM⊥AC.则ON=OAsin∠MAO=
| ||
|
在Rt△B1ON中,tan∠B1NO=
| B1O |
| ON |
| 5 |
∴∠B1NO=arctan
| 5 |
| 5 |
看了 如图,正方体AC1中,已知O...的网友还看了以下:
分子晶体 原子晶体 离子晶体3、下列物质的液体中,不存在分子是A 二氧化硅 B 二氧化硫 C 二氧 2020-05-16 …
锦葵科的雄蕊类型是()。A.二体雄蕊B.单体雄蕊C.多体雄蕊D.四强雄蕊 2020-05-25 …
菊科的雄蕊是()。A.二体雄蕊B.单体雄蕊C.多体雄蕊D.聚药雄蕊 2020-05-25 …
蝶形花科的雄蕊是()。A.二体雄蕊B.单体雄蕊C.多体雄蕊D.聚药雄蕊 2020-05-25 …
罐体对进行温度修正是指对( )进行热胀冷缩修正.A.罐体钢板B.罐内油品C.检尺D.罐内气体空间 2020-05-31 …
有一个正十二面体,12个面上分别写有1~12这12个整数投掷这个正十二面体一次求下有一个正十二面体 2020-06-06 …
求正多面体体积和表面积公式正四面体、正六面体、正八面体的公式比较简单,一齐写出来吧而求正十二面体、 2020-06-07 …
下列叙述不正确(A)A,二倍体*二倍体-二倍体B,三倍体*三倍体-三倍体C,二倍体*四倍体-三倍体 2020-06-10 …
立体图形旋转对称求正方体正四面体正八面体正六棱柱正四棱缀正十二面体正二十面体等有多少条旋转对称轴和 2020-06-21 …
怎么用grasshopper在球面上均匀布点?我知道了,只存在五种正多面体,正四面体、正六面体(正 2020-08-02 …