早教吧作业答案频道 -->数学-->
过正三棱锥的侧棱与底面中心作截面,已知截面是以侧棱为底边的等腰三角形,若侧面与底面所成的角为θ,则cosθ=.
题目详情
过正三棱锥的侧棱与底面中心作截面,已知截面是以侧棱为底边的等腰三角形,若侧面与底面所成的角为θ,则cosθ=___.
▼优质解答
答案和解析
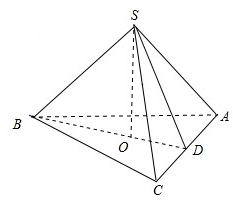 延长BO交AC于D,则D为AC中点.截面为△SBD.
延长BO交AC于D,则D为AC中点.截面为△SBD.
由正棱锥的性质,SO⊥面ABC,SD⊥AC,BD⊥AC,∠SDB为侧面和底面所成角的平面角.设底面边长BC=2.
∵SD=BD,∴SC=BC,
∵正三棱锥S-ABC为正四面体.
∴BD=
,
在△SDB中,由余弦定理得cos∠SDB=
=
.
故答案为
 延长BO交AC于D,则D为AC中点.截面为△SBD.
延长BO交AC于D,则D为AC中点.截面为△SBD.由正棱锥的性质,SO⊥面ABC,SD⊥AC,BD⊥AC,∠SDB为侧面和底面所成角的平面角.设底面边长BC=2.
∵SD=BD,∴SC=BC,
∵正三棱锥S-ABC为正四面体.
∴BD=
| 3 |
在△SDB中,由余弦定理得cos∠SDB=
| 3+3-4 | ||||
2×
|
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
看了 过正三棱锥的侧棱与底面中心作...的网友还看了以下:
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.已知同底的两个正三棱锥内接于同一个球.已 2020-04-24 …
如图所示,在边长为5+2的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为 2020-04-27 …
妈妈对我的关心真是无微不至为开头的为中心句写一段话 2020-05-16 …
企业评估以企业的( )为核心。 A.生产能力B.获利能力C.偿债能力D.资产周转能力 2020-05-19 …
弄斧必到班门阅读答案“弄斧必到班门”这句话,是数学家华罗庚说的,是他的为学心得.当时,我问他近期有 2020-06-09 …
若一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥.已知一个正六棱 2020-06-27 …
(12分)圆、椭圆、双曲线都有对称中心,统称为有心圆锥曲线,它们统一的标准方程为.圆的很多优美性质 2020-08-01 …
芦笋享有“蔬菜之王”的美称,为百合科植物石刁柏的嫩芽,外形与禾本科植物芦苇的嫩芽相似,嫩茎中间组织呈 2020-11-11 …
某贪官的“为官心得”是:“升官不发财,请我都不来;当官不收钱,退了没本钱。”从这一贪官的言行中,我们 2020-11-23 …
某贪官的“为官心得”是:“升官不发财,请我都不来;当官不收钱,退了没本钱。”从这一贪官的言行中,我们 2020-11-23 …