早教吧作业答案频道 -->数学-->
已知一个圆锥内接于球O(圆锥的底面圆周及顶点均在球面上),若球的表面积为100π,圆锥的高是底面半径的2倍,则圆锥的高为.
题目详情
已知一个圆锥内接于球O(圆锥的底面圆周及顶点均在球面上),若球的表面积为100π,圆锥的高是底面半径的2倍,则圆锥的高为___.
▼优质解答
答案和解析
设圆锥的底面半径为r,圆锥的高h=2r,球的半径R,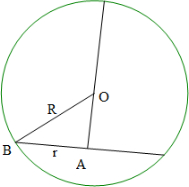
则4πR2=100π,解得R=5.
设圆锥底面中心为A,圆锥底面圆周上一点为B,
则OA=2r-5,OB=5,AB=r.
∴r2+(2r-5)2=25,解得r=4或r=0(舍).
∴h=2r=8.
故答案为:8.

则4πR2=100π,解得R=5.
设圆锥底面中心为A,圆锥底面圆周上一点为B,
则OA=2r-5,OB=5,AB=r.
∴r2+(2r-5)2=25,解得r=4或r=0(舍).
∴h=2r=8.
故答案为:8.
看了 已知一个圆锥内接于球O(圆锥...的网友还看了以下:
A1、B1、C1、D1四个单元格的数字,要求如下:任意2个大于0,1个小于0,1个等于0(2个大于 2020-05-13 …
有一个100匝的线圈,在0.2秒内穿过它的磁通量从0.01wb增加到0.05wb求线圈中感应电动势 2020-05-23 …
已知命题p:"如果函数y=f(x)在(a,b)内可导,在[a,b]上连续(图像不间断),且f(a) 2020-06-04 …
已知f(x)=cosx在[0,2π]连续,在[0,2π]内可导,且f(0)=f(2π)=1,所以存 2020-06-04 …
已知函数f(x)是定义在[-2,2]上的奇函数,且在[0,2]内有3个零点,则函数在[-2,2]已 2020-06-09 …
高等数学介值定理证明题目设f(x)在[0,π/2]上的一阶导数连续,在(0,π/2)内二阶可导,且 2020-06-10 …
设f(x)在[0,2]上连续,在(0,2)内可导,3f(0)=2f(1)+f(2).求存在一点令a 2020-06-18 …
已知f(x)是周期为1的周期函数,在[0,1)上,f(x)=x^2,求f(x)在[0,2]上的表达 2020-07-23 …
请教2个关于三角函数的问题(1)若关于x的方程3sinx+4cosx=a在区间(0,2π)内有两个 2020-07-30 …
如何判断一个区间如:10-18在0-2,2-9,9-24之间的算法小弟不才,想请各位高手赐教:我要求 2020-11-15 …