早教吧作业答案频道 -->数学-->
如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.(1)求证:BD∥平面FGH;(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
题目详情
如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
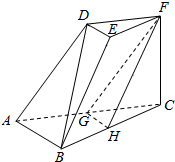
(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.

(1)求证:BD∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
▼优质解答
答案和解析
(I)证法一:如图所示,连接DG,CD,设CD∩GF=M,连接MH.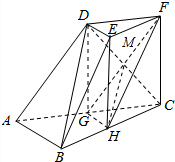
在三棱台DEF-ABC中,AB=2DE,G为AC的中点.
∴DF
GC,∴四边形CFDG是平行四边形,
∴DM=MC.又BH=HC,
∴MH∥BD,又BD⊄平面FGH,MH⊂平面FGH,
∴BD∥平面FGH;
证法二:在三棱台DEF-ABC中,AB=2DE,H为BC的中点.
∴BH
EF,
∴四边形BHFE为平行四边形.
∴BE∥HF.
在△ABC中,G为AC的中点,H为BC的中点,
∴GH∥AB,又GH∩HF=H,
∴平面FGH∥平面ABED,
∵BD⊂平面ABED,∴BD∥平面FGH.
(II)证明:连接HE,∵G,H分别为AC,BC的中点,
∴GH∥AB,
∵AB⊥BC,∴GH⊥BC,
又H为BC的中点,∴EF∥HC,EF=HC.
∴EFCH是平行四边形,∴CF∥HE.
∵CF⊥BC,∴HE⊥BC.
又HE,GH⊂平面EGH,HE∩GH=H,
∴BC⊥平面EGH,又BC⊂平面BCD,
∴平面BCD⊥平面EGH.

在三棱台DEF-ABC中,AB=2DE,G为AC的中点.
∴DF
| ∥ |
. |
∴DM=MC.又BH=HC,
∴MH∥BD,又BD⊄平面FGH,MH⊂平面FGH,
∴BD∥平面FGH;
证法二:在三棱台DEF-ABC中,AB=2DE,H为BC的中点.
∴BH
| ∥ |
. |
∴四边形BHFE为平行四边形.
∴BE∥HF.
在△ABC中,G为AC的中点,H为BC的中点,
∴GH∥AB,又GH∩HF=H,
∴平面FGH∥平面ABED,
∵BD⊂平面ABED,∴BD∥平面FGH.
(II)证明:连接HE,∵G,H分别为AC,BC的中点,
∴GH∥AB,
∵AB⊥BC,∴GH⊥BC,
又H为BC的中点,∴EF∥HC,EF=HC.
∴EFCH是平行四边形,∴CF∥HE.
∵CF⊥BC,∴HE⊥BC.
又HE,GH⊂平面EGH,HE∩GH=H,
∴BC⊥平面EGH,又BC⊂平面BCD,
∴平面BCD⊥平面EGH.
看了 如图,三棱台DEF-ABC中...的网友还看了以下:
把一副三角尺(30°,60°,90°,和45°,45°,90°)如图(甲)放置在平面直角坐标系中, 2020-04-13 …
1.正三棱锥P-ABC的四个顶点同在一个半径为2的球面上,若正三棱锥的侧棱长为2√3,则正三棱锥的 2020-04-24 …
如图,在正方形ABCD中,CE垂直于DF,交点为G,若CE=10cm,求DF的长条件充足,卷子上就 2020-05-15 …
∠ADC=∠ABC、∠1+∠2=180DA是∠FDB的平分线说明BC是∠DBE的平分线将一张长方形 2020-06-27 …
接到后面出现超越方程,谢谢伸出援手g(x)=2lnx-ax^2+x-e/a+1/2,当a>0时讨论 2020-06-27 …
(2012•房山区一模)在直三棱柱ABC-A1B1C1中,BC=CC1=AB=2,AB⊥BC.点M 2020-07-09 …
已知E为平行四边形ABCD中DC边的延长线上的一点,且CE=CD,连结AE分别交BC,BD于点F,G 2020-11-03 …
已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则”。若把该结论推广到空 2020-11-22 …
已知函数,函数g(x)=f2(x)+f(x)+t(t∈R).关于g(x)的零点,下列判断不正确的是( 2020-12-24 …
如图,在正方形ABCD中,G是BC上的任意一点(G与B,C两点不重合),E,F是AG上的两点(E,F 2021-01-11 …