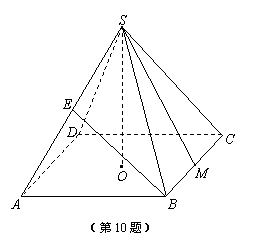
正四棱锥S-ABCD中,O为底面中心,E为SA的中点,AB=1,直线AD到平面SBC的距离等于.(1)求斜高SM的长;(2)求平面EBC与侧面SAD所成锐二面角的大小
正四棱锥 S - ABCD 中, O 为底面中心, E 为 SA 的中点, AB =1,直线 AD 到平面 SBC 的距离等于 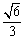 .
.
(1)求斜高 SM 的长;
(2)求平面 EBC 与侧面 SAD 所成锐二面角的大小
二次函数中的b在函数中起什么作用?比如说函数y=x^2+bx+中b的值从-1到1变化,那么函数的图象 2020-03-30 …
硼(B)有两种同位素,一种核内有5个中子,另一种核内有6个中子,B的相对原子质量是10.8,求自然 2020-06-23 …
A、B两物体相距7米,其中A以4米每秒向右匀速运动,B以10米每秒在摩擦力作用下向右做匀减速运动, 2020-07-14 …
已知,如图,a,b,c分别是△ABC中∠A,∠B,∠C的对边,P为BC上一点,以AP为直径的圆O交 2020-07-19 …
在Rt△ABC中,锐角A的平分线与锐角B的邻补角的平分线相交于点D,则∠ADB=度. 2020-07-21 …
如图表示人体细胞中重要有机物A、B、C、D、E的元素组成及相互关系,据图回答:(1)a、b、c分别 2020-07-25 …
在N=log(5-b)(b-2)中b的取值范围(5-b)是底数(b-2)是真数 2020-11-17 …
如图是胰腺组织局部结构模式图,请据图回答:(1)试用箭头表示图中A、B、C三中液体之间的关系其稳态是 2020-12-17 …
A、B、C、D、E是相邻三个周期中的五种元素,它们的原子序数依次增大,B、C、D属同一周期,A、E在 2021-01-05 …
A、B、C、D、E是相邻三个周期中的五种元素,它们的原子序数依次增大,B、C、D属同一周期,A、E在 2021-01-05 …