早教吧作业答案频道 -->数学-->
如图,在正三棱柱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.(1)若M、N分别是CC1、AB的中点,求证:CN∥平面AB1M;(2)求证:不论M在何位置,三棱锥A1-A
题目详情
如图,在正三棱柱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M是棱CC1上一点.
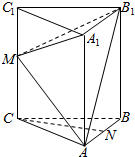
(1)若M、N分别是CC1、AB的中点,求证:CN∥平面AB1M;
(2)求证:不论M在何位置,三棱锥A1-AMB1的体积都为定值,并求出该定值.

(1)若M、N分别是CC1、AB的中点,求证:CN∥平面AB1M;
(2)求证:不论M在何位置,三棱锥A1-AMB1的体积都为定值,并求出该定值.
▼优质解答
答案和解析
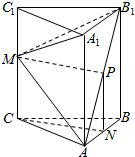 证明:(1)取AB1中点P,连结MP,NP,
证明:(1)取AB1中点P,连结MP,NP,
∵P是AB1的中点,N是AB的中点,∴PN∥BB1,PN=
BB1,
∵M是CC1的中点,∴CM∥BB1,CM=
BB1,
∴CM∥PN,CM=PN,∴四边形MCNP是平行四边形,
∴CN∥MP,∵MP⊂平面AB1M,CN⊄AB1M,
∴CN∥平面AB1M.
(2)∵△ABC是等边三角形,∴CN⊥AB,
∵BB1⊥平面ABC,PN∥BB1,
∴PN⊥平面ABC,∵CN⊂平面ABC,
∴PN⊥CN,又∵AB⊂平面ABB1A1,PN⊂平面ABB1A1,AB∩PN=N,
∴CN⊥平面AB1BA1,
∵CN=
=3
.
∴V 棱锥A1-AMB1=V 棱锥M-AA1B1=
S △AA1B1•CN=
×
×6×6×3
=18
.
∴不论M在何位置,三棱锥A1-AMB1的体积都为定值18
.
 证明:(1)取AB1中点P,连结MP,NP,
证明:(1)取AB1中点P,连结MP,NP,∵P是AB1的中点,N是AB的中点,∴PN∥BB1,PN=
| 1 |
| 2 |
∵M是CC1的中点,∴CM∥BB1,CM=
| 1 |
| 2 |
∴CM∥PN,CM=PN,∴四边形MCNP是平行四边形,
∴CN∥MP,∵MP⊂平面AB1M,CN⊄AB1M,
∴CN∥平面AB1M.
(2)∵△ABC是等边三角形,∴CN⊥AB,
∵BB1⊥平面ABC,PN∥BB1,
∴PN⊥平面ABC,∵CN⊂平面ABC,
∴PN⊥CN,又∵AB⊂平面ABB1A1,PN⊂平面ABB1A1,AB∩PN=N,
∴CN⊥平面AB1BA1,
∵CN=
| AC2-AN2 |
| 3 |
∴V 棱锥A1-AMB1=V 棱锥M-AA1B1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∴不论M在何位置,三棱锥A1-AMB1的体积都为定值18
| 3 |
看了 如图,在正三棱柱ABC-A1...的网友还看了以下:
高二圆锥曲线,过椭圆的左焦点,倾斜角为60度的直线,交椭圆于A,B两点,且AF=2FB,求椭圆的离心 2020-03-30 …
如图所示,直线AD、CD、BC两两垂直,且AD与BC不在同一平面内.已知BC=3,CD=4,AB= 2020-05-13 …
在三角形ABC中,AB=8,AC=6,点D在AC上,且AD=2,如果在AB上找一点E,使三角形AD 2020-05-15 …
已知A-BCD是棱长都相等的三棱锥,E为AC的中点,F在AD上,且AF/FD=1/2,请问:二面角 2020-05-23 …
在直角三角ABC中,角A等于90度,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接O 2020-06-06 …
在△ABC中,满足:AB⊥AC,M是BC的中点.1.若向量|AB|=向量|AC|,求AB+2AC与 2020-06-12 …
放置于椎体内的水的高度为h1,且水面高是椎体高的1/3一个封闭的圆锥容器,当锥顶向上时,放置于椎体 2020-06-21 …
下列命题中正确的是()①底面是正多边形的棱锥是正棱锥②侧棱都相等的棱锥是正棱锥③侧面是等腰三角形的 2020-06-27 …
如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( ) A 2020-06-27 …
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.(1)分别以直线AC、BC为轴,把△AB 2020-07-01 …