早教吧作业答案频道 -->数学-->
如图,在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q.(1)求证:PQ∥平面ABC1;(2)若AB=AA1,BC=3,AC1=3,BC1=13,求证:平面ABC1⊥平面AA1C1C.
题目详情
如图,在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q.
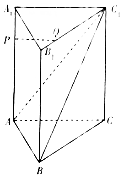
(1)求证:PQ∥平面ABC1;
(2)若AB=AA1,BC=3,AC1=3,BC1=
,求证:平面ABC1⊥平面AA1C1C.

(1)求证:PQ∥平面ABC1;
(2)若AB=AA1,BC=3,AC1=3,BC1=
| 13 |
▼优质解答
答案和解析
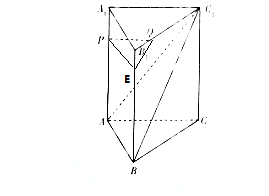 证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,
证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,
∵在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q,
∴PE∥AB,QE∥BC1,
∵AB∩BC1=B,PE∩QE=E,AB、BC1⊂平面ABC1,
PE、QE⊂平面PQE,
∴平面ABC1∥平面PQE,
∵PQ⊂平面PQE,∴PQ∥平面ABC1.
(2)∵在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,
∴AB⊥CC1,BC⊥CC1,
∵AB=AA1,BC=3,AC1=3,BC1=
,
∴AB=AA1=CC1=
=2,AC=
=
=
,
∴AB2+AC2=BC2,∴AB⊥AC,
又AC∩CC1=C,∴AB⊥平面AA1C1C,
∵AB⊂平面ABC1,∴平面ABC1⊥平面AA1C1C.
 证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,
证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,∵在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q,
∴PE∥AB,QE∥BC1,
∵AB∩BC1=B,PE∩QE=E,AB、BC1⊂平面ABC1,
PE、QE⊂平面PQE,
∴平面ABC1∥平面PQE,
∵PQ⊂平面PQE,∴PQ∥平面ABC1.
(2)∵在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,
∴AB⊥CC1,BC⊥CC1,
∵AB=AA1,BC=3,AC1=3,BC1=
| 13 |
∴AB=AA1=CC1=
| 13-9 |
| AC12-CC12 |
| 9-4 |
| 5 |
∴AB2+AC2=BC2,∴AB⊥AC,
又AC∩CC1=C,∴AB⊥平面AA1C1C,
∵AB⊂平面ABC1,∴平面ABC1⊥平面AA1C1C.
看了 如图,在直三棱柱ABC-A1...的网友还看了以下:
时间表示法中的B.C.,A.D.和A.I.(比如500B.C.,750A.D.,2025A.I.)分 2020-03-30 …
excel表中,如下所述,怎么实现?在A列写公式,假设A列A1为1,共有1000行.在B.C.D. 2020-04-06 …
GBK码的‘B.C.F换成数字是多少 2020-05-15 …
已知二次函数f(x)=ax^2+bx+c图像如图所示,记p=[a-b+c]+[2a+b],q=[a 2020-05-15 …
已知向量a,b,c满足|a|=1,|a-b|=|b|,(a-c)(b-c)=0.若对每一确定的b, 2020-05-16 …
二次函数的B,C求值已知抛物线Y=X的平方+BX+C与X轴只有1个交点,且交点为A(2,0)求B, 2020-05-21 …
A球带+q的电B球带-q的电,C球不带电,将A球B球固定,让C球和A球接触,再跟B接触,最后拿掉. 2020-05-23 …
语句A,ACL10的B,C和D已经输入的显示顺序和程序;灭蝇灯接口E0入境,以防止所有主机(除了那些 2020-05-31 …
圆O过锐角三角形ABC的B,C交AB,AC于E,F另一等圆过A,E,F则圆O过三角形ABC的内心外 2020-06-03 …
英文中的b/c和应该是年轻人流行的简写的俚语类的吧?谢谢英语强人们!我常在我的一些美国朋友的博客里 2020-06-07 …