在直角坐标系xOy中，直线l的方程是y=8，圆C的参数方程是x=2+2cosφy=2sinφ（φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．（1）求直线l和圆C的极坐标方程；（2）射线OM：θ=α（

Question

在直角坐标系xOy中，直线l的方程是y=8，圆C的参数方程是

x=2+2cosφ

y=2sinφ

（φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求直线l和圆C的极坐标方程；
（2）射线OM：θ=α（其中0<α<(π)/(2)）与圆C交于O，P两点，与直线l交于点M，直线ON：θ=α+(π)/(2)与圆C交于O，Q两点，与直线l交于点N，求(|OP|)/(|OM|)•(|OQ|)/(|ON|)的最大值．

Answer 1

（1）直线l的方程是y=8，化为极坐标方程为：ρsinθ=8．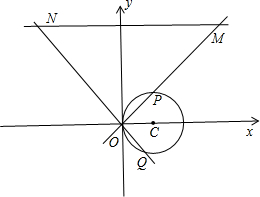
圆C的参数方程是

x=2+2cosφ

y=2sinφ

（φ为参数），化为普通方程：（x-2）²+y²=4，
展开为：x²+y²-4x=0，化为极坐标方程：ρ²-4ρcosθ=0，即ρ=4cosθ．
（2）(|OP|)/(|OM|)•(|OQ|)/(|ON|)=(4cosα)/((8)/(sinα))•(-4cos(α+(π)/(2)))/((8)/(sin(α+(π)/(2))))=(1)/(16)sin2(2α)≤(1)/(16)（2α∈（0，π））．
∴(|OP|)/(|OM|)•(|OQ|)/(|ON|)的最大值为(1)/(16)．