已知在平面直角坐标系xOy中，以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C1的极坐标方程为ρ=4cosθ，直线l的参数方程为（t为参数）．（1）求曲线C1的直角坐标方程及直

Question

已知在平面直角坐标系xOy中，以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C₁的极坐标方程为ρ=4cosθ，直线l的参数方程为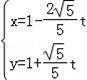（t为参数）．

（1）求曲线C₁的直角坐标方程及直线l的普通方程；

（2）若曲线C₂的参数方程为（α为参数），曲线C₁上点P的极角为，Q为曲线C₂上的动点，求PQ的中点M到直线l距离的最大值．

　

Answer 1

【考点】简单曲线的极坐标方程；参数方程化成普通方程．

【分析】（1）曲线C₁的极坐标方程为ρ=4cosθ，即ρ²=4ρcosθ，可得直角坐标方程．直线l的参数方程为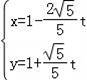（t为参数），消去参数t可得普通方程．

（2），直角坐标为（2，2），，利用点到直线的距离公式及其三角函数的单调性可得最大值．

【解答】（1）曲线C₁的极坐标方程为ρ=4cosθ，即ρ²=4ρcosθ，

可得直角坐标方程：．

直线l的参数方程为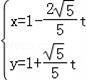（t为参数），

消去参数t可得普通方程：x+2y﹣3=0．

（2），直角坐标为（2，2），，

∴M到l的距离≤，

从而最大值为．