早教吧作业答案频道 -->数学-->
已知椭圆C:(a>b>0)的右准线l的方程为x=,短轴长为2.(1)求椭圆C的方程;(2)过定点B(1,0)作直线l与椭圆C相交于P,Q(异于A1,A2)两点,设直线PA1与直线QA2相交于
题目详情
已知椭圆C: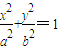 (a>b>0)的右准线l的方程为x=
(a>b>0)的右准线l的方程为x=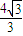 ,短轴长为2.
,短轴长为2.
(1)求椭圆C的方程;
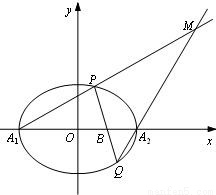
(2)过定点B(1,0)作直线l与椭圆C相交于P,Q(异于A 1 ,A 2 )两点,设直线PA 1 与直线QA 2 相交于点M(2x ,y ).
①试用x ,y 表示点P,Q的坐标;
②求证:点M始终在一条定直线上.
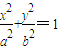 (a>b>0)的右准线l的方程为x=
(a>b>0)的右准线l的方程为x=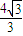 ,短轴长为2.
,短轴长为2.(1)求椭圆C的方程;
(2)过定点B(1,0)作直线l与椭圆C相交于P,Q(异于A 1 ,A 2 )两点,设直线PA 1 与直线QA 2 相交于点M(2x ,y ).
①试用x ,y 表示点P,Q的坐标;
②求证:点M始终在一条定直线上.

▼优质解答
答案和解析
分析:
(1)由题设条件能够得到,由此可求出椭圆C的方程.(2)A1(-2,0),A2(2,0),方程为MA1的方程为:,代入,得.P(,).同理可得Q(,).再由P,Q,B三点共线,知kPB=kQB,从而得到点M始终在定直线x=4上.
(1)由得∴椭圆C的方程为;(2)A1(-2,0),A2(2,0),方程为MA1的方程为:,即.代入,得,即.∴=,则=.即P(,).同理MA2的方程为,即.代入,得,即.∴=.则=.即Q(,).∵P,Q,B三点共线,∴kPB=kQB,即.∴.即.由题意,y≠0,∴.3(x+1)(x-1)2-(x+1)y2=(x-1)(x+1)2-3(x-1)y2.∴(2x-4)(x2+y2-1)=0.则2x-4=0或x2+y2=1.若x2+y2=1,即,则P,Q,M为同一点,不合题意.∴2x-4=0,点M始终在定直线x=4上.
点评:
本题考查直线和圆锥曲线的综合应用,解题时要认真审题,仔细解答,注意培养计算能力.
分析:
(1)由题设条件能够得到,由此可求出椭圆C的方程.(2)A1(-2,0),A2(2,0),方程为MA1的方程为:,代入,得.P(,).同理可得Q(,).再由P,Q,B三点共线,知kPB=kQB,从而得到点M始终在定直线x=4上.
(1)由得∴椭圆C的方程为;(2)A1(-2,0),A2(2,0),方程为MA1的方程为:,即.代入,得,即.∴=,则=.即P(,).同理MA2的方程为,即.代入,得,即.∴=.则=.即Q(,).∵P,Q,B三点共线,∴kPB=kQB,即.∴.即.由题意,y≠0,∴.3(x+1)(x-1)2-(x+1)y2=(x-1)(x+1)2-3(x-1)y2.∴(2x-4)(x2+y2-1)=0.则2x-4=0或x2+y2=1.若x2+y2=1,即,则P,Q,M为同一点,不合题意.∴2x-4=0,点M始终在定直线x=4上.
点评:
本题考查直线和圆锥曲线的综合应用,解题时要认真审题,仔细解答,注意培养计算能力.
看了 已知椭圆C:(a>b>0)的...的网友还看了以下:
设ab是两条异面直线,P是ab外的一点,则下列结论正确的是()A.过P有一条直线和ab都平行B.过 2020-05-13 …
如图所示,竖直平面内固定着一个滑槽轨道,其左半部是倾角为θ=37°,长为l=1m的斜槽PQ,右部是 2020-05-13 …
设服从二项分布B~(n,p)的随机变量ξ的期望和方差分别是2.4与1.44,则二项分布的参数n、p 2020-05-15 …
设O为坐标原点,曲线X^2+Y^2+2X-6Y+1=0 上有2点P Q,满足关于直线X+MY+4= 2020-06-27 …
一弹簧秤的称盘质量M1=1.5Kg,盘内放一物体P,P的质量M2=10.5Kg.弹簧质量不计.其劲 2020-06-30 …
定义点P(x0,y0)到直线l:Ax+By+C=0(A2+B2≠0)的有向距离为d=Ax0+By0 2020-07-09 …
t为何值时,PQ与圆O相切直角梯形ABCDAD平行BC中,角ABC等于90度,AB等于12,AD等 2020-07-26 …
判断下列各对直线是否垂直:(1)y=x,2x+2y-7=0(2)x+4y-5=0,4x-3y-5= 2020-08-01 …
经过下列语句intj,a[10],*p;定义后,下列语句合法的是()A.p=p+2B.p=经过下列语 2020-11-06 …
如图,直线l与x轴、y轴分别相交于A、B两点,已知B(0,3),∠BAO=30°,圆心P的坐标为(1 2021-01-11 …