已知椭圆C：+=1（a＞b＞0）的离心率为，焦点与短轴的两顶点的连线与圆x2+y2=相切．（Ⅰ）求椭圆C的方程；（Ⅱ）过点（1，0）的直线l与C相交于A，B两点，在x轴上是否存在点N，使得

Question

已知椭圆C： +=1（a＞b＞0）的离心率为，焦点与短轴的两顶点的连线与圆x²+y²=相切．

（Ⅰ）求椭圆C的方程；

（Ⅱ）过点（1，0）的直线l与C相交于A，B两点，在x轴上是否存在点N，使得•为定值？如果有，求出点N的坐标及定值；如果没有，请说明理由．

Answer 1

【考点】椭圆的简单性质．

【分析】（Ⅰ）由椭圆的离心率为，焦点与短轴的两顶点的连线与圆x²+y²=相切，列出方程组，求出a，b，由此能求出椭圆方程．

（Ⅱ）当直线l的斜率存在时，设其方程为y=k（x﹣1），A（x₁，y₁），B（x₂，y₂），直线方程与椭圆立，利用韦达定理、根的判别式、向量的数量积，结合已知条件能求出存在点满足．

【解答】（Ⅰ）∵椭圆C： +=1（a＞b＞0）的离心率为，焦点与短轴的两顶点的连线与圆x²+y²=相切，

∴，

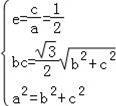
解得c²=1，a²=4，b²=3

∴椭圆方程为

（Ⅱ）当直线l的斜率存在时，设其方程为y=k（x﹣1），A（x₁，y₁），B（x₂，y₂），

则△＞0，，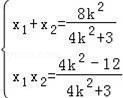

若存在定点N（m，0）满足条件，

则有=（x₁﹣m）（x₂﹣m）+y₁y₂

=

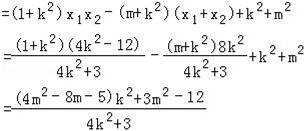
如果要上式为定值，则必须有

验证当直线l斜率不存在时，也符合．

故存在点满足