椭圆x2a2+y2b2=1(a>b>0)的一个焦点为F，该椭圆上有一点A，满足△OAF是等边三角形（O为坐标原点），则椭圆的离心率是（）A.3-1B.2-3C.2-1D.2-2

Question

椭圆

(x2)/(a2)+(y2)/(b2)=1(a>b>0)的一个焦点为F，该椭圆上有一点A，满足△OAF是等边三角形（O为坐标原点），则椭圆的离心率是（　　）

A.

√(3)-1

B. 2-

√(3)

C.

√(2)-1

D. 2-

√(2)

Answer 1

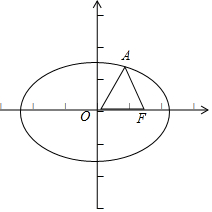根据题意，如图，设F（0，c），
又由△OAF是等边三角形，则A（(c)/(2)，(√(3)c)/(2)），
A在椭圆上，则有(c2)/(4a2)+(3c2)/(4b2)=1，①；
a²=b²+c²，②；
联立①②，解可得c=（√(3)-1）a，
则其离心率e=(c)/(a)=√(3)-1；
故选：A．