已知椭圆x2a2+y2b2=1（a>b>0）的左、右焦点分别为F1，F2，过F2作一条直线（不与x轴垂直）与椭圆交于A，B两点，如果△ABF1恰好为等腰直角三角形，该直线的斜率为（）A.±1B.±2C.±2D.

Question

已知椭圆

(x2)/(a2)+(y2)/(b2)=1（a>b>0）的左、右焦点分别为F₁，F₂，过F₂作一条直线（不与x轴垂直）与椭圆交于A，B两点，如果△ABF₁恰好为等腰直角三角形，该直线的斜率为（　　）

A. ±1

B. ±2

C. ±

√(2)

D. ±

√(3)

Answer 1

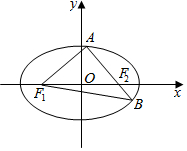可设|F₁F₂|=2c，|AF₁|=m，
若△ABF₁构成以A为直角顶点的等腰直角三角形，
则|AB|=|AF₁|=m，|BF₁|=√(2)m，
由椭圆的定义可得△ABF₁的周长为4a，
即有4a=2m+√(2)m，即m=2（2-√(2)）a，
∴|AF₁|=2（2-√(2)）a，
则|AF₂|=2a-m=（2√(2)-2）a，
在Rt△AF₁F₂中，
tan∠AF₂F₁=(丨AF1丨)/(丨AF2丨)=√(2)，
∴直线AB的斜率为k=±tan∠AF₂F₁=±√(2)，
故选：C．