早教吧作业答案频道 -->数学-->
如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.(1)求线段AB的中点P的轨迹;(2)在线段AB上取一点Q,使,求点Q的轨迹.
题目详情
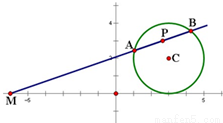
如图所示,过点M(-6,0)作圆C:x 2 +y 2 -6x-4y+9=0的割线,交圆C于A、B两点.
(1)求线段AB的中点P的轨迹;
(2)在线段AB上取一点Q,使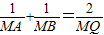 ,求点Q的轨迹.
,求点Q的轨迹.
(1)求线段AB的中点P的轨迹;
(2)在线段AB上取一点Q,使
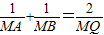 ,求点Q的轨迹.
,求点Q的轨迹.
▼优质解答
答案和解析
分析:
(1)设中点P的坐标,建立关于点P的方程,从而确定轨迹方程.(2)利用代入法求点点Q的轨迹.
(1)圆C的方程为(x-3)2+(y-2)2=4,其圆心为C(3,2),半径为2.又M∈{M|PC⊥MP,P在已知圆内},设P点坐标(x,y),则CP的斜率为,MP的斜率为,所以,化简得x2+y2+3x-2y-18=0.点C(3,2)应在轨迹上,而x=3时,y=2满足方程x2+y2+3x-2y-18=0,所以点P的轨迹是圆x2+y2+3x-2y-18=0在已知圆内的一段弧.(2)设A(x1,y1),B(x2,y2),Q(x,y),直线AB的斜率为k,则有,代入,有,即,①把y=k(x+6)代入x2+y2-6x-4y+9=0,得(k2+1)x2+2(6k2-2k-3)x+3(12k2-8k+3)=0,,②②代入①并化简得,而,从而有9x+2y-27=0,所以点Q的轨迹是直线9x+2y-27=0的圆内部分.
点评:
本题考查直线与圆的位置关系,考查轨迹方程,运算量较大,综合性较强.
分析:
(1)设中点P的坐标,建立关于点P的方程,从而确定轨迹方程.(2)利用代入法求点点Q的轨迹.
(1)圆C的方程为(x-3)2+(y-2)2=4,其圆心为C(3,2),半径为2.又M∈{M|PC⊥MP,P在已知圆内},设P点坐标(x,y),则CP的斜率为,MP的斜率为,所以,化简得x2+y2+3x-2y-18=0.点C(3,2)应在轨迹上,而x=3时,y=2满足方程x2+y2+3x-2y-18=0,所以点P的轨迹是圆x2+y2+3x-2y-18=0在已知圆内的一段弧.(2)设A(x1,y1),B(x2,y2),Q(x,y),直线AB的斜率为k,则有,代入,有,即,①把y=k(x+6)代入x2+y2-6x-4y+9=0,得(k2+1)x2+2(6k2-2k-3)x+3(12k2-8k+3)=0,,②②代入①并化简得,而,从而有9x+2y-27=0,所以点Q的轨迹是直线9x+2y-27=0的圆内部分.
点评:
本题考查直线与圆的位置关系,考查轨迹方程,运算量较大,综合性较强.
看了 如图所示,过点M(-6,0)...的网友还看了以下:
过圆C:x2+y2=4上一动点M作x轴的垂线段MD,D为垂足.若MD=2MQ.(1)求动点Q的轨迹 2020-04-13 …
在直角坐标系xoy中,点m到点F1(-根号3,0),F2(根号3,0)的距离之和是4,点M的轨迹C 2020-05-16 …
(2001•上海)如图,已知椭圆C的方程为x2+y22=1,点P(a,b)的坐标满足a2+b22≤ 2020-06-14 …
如下图,有一小球从P点以相同的初速度可经三条不同的光滑轨道向Q点运动,其中A轨道为先上坡再下坡的形 2020-07-21 …
如图,倾斜固定的气垫导轨底端固定有滑块P,滑块Q可在导轨上无摩擦滑动,两滑块上分别固定有同名磁极相 2020-07-28 …
如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.(1 2020-07-31 …
如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.(1 2020-07-31 …
如图所示,点电荷Q固定,虚线是带电量为q的微粒的运动轨迹,微粒的重力不计,a、b是轨迹上的两个点,b 2020-12-05 …
如图所示,两个相同的弧形轨道M、N,分别用于发射小铁球P、Q,两轨道上端分别装有电磁铁C、D.调C、 2020-12-25 …
(1)如图1的装置中,两个相同的弧形轨道M、N,分别用于发射小铁球P、Q,两轨道上分别装有电磁铁C、 2020-12-25 …