早教吧作业答案频道 -->数学-->
如图,AH是O的直径,AE平分∠FAH,交O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.(1)求证:直线FG是O的切线;(2)若CD=10,EB=5,求O的直径
题目详情
如图,AH是 O的直径,AE平分∠FAH,交 O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
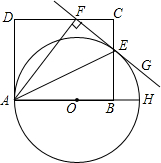
(1)求证:直线FG是 O的切线;
(2)若CD=10,EB=5,求 O的直径.

(1)求证:直线FG是 O的切线;
(2)若CD=10,EB=5,求 O的直径.
▼优质解答
答案和解析
(1)如图1,连接OE,
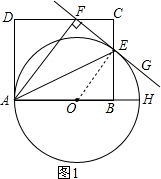
∵OA=OE,
∴∠EAO=∠AEO,
∵AE平分∠FAH,
∴∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
∵AF⊥GF,
∴∠AFE=∠OEF=90°,
∴OE⊥GF,
∵点E在圆上,OE是半径,
∴GF是 O的切线.
(2)∵四边形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
设OA=OE=x,则OB=10-x,
在Rt△OBE中,∠OBE=90°,BE=5,
由勾股定理得:OB2+BE2=OE2,
∴(10-x)2+52=x2,
∴x=
,
AH=2×
=
,
∴ O的直径为
.

∵OA=OE,
∴∠EAO=∠AEO,
∵AE平分∠FAH,
∴∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
∵AF⊥GF,
∴∠AFE=∠OEF=90°,
∴OE⊥GF,
∵点E在圆上,OE是半径,
∴GF是 O的切线.
(2)∵四边形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
设OA=OE=x,则OB=10-x,
在Rt△OBE中,∠OBE=90°,BE=5,
由勾股定理得:OB2+BE2=OE2,
∴(10-x)2+52=x2,
∴x=
| 25 |
| 4 |
AH=2×
| 25 |
| 4 |
| 25 |
| 2 |
∴ O的直径为
| 25 |
| 2 |
看了 如图,AH是O的直径,AE平...的网友还看了以下:
设a>1,b>0,a的b平方+a的-b平方=2根号2则a的b平方-a的-b平方= 2020-04-05 …
关于牛顿第一定律,以下说法不正确的是:A平时所见的静止物体是符合牛顿第一定律所阐述的情况的B平时所 2020-04-27 …
若0.5加a的和的平方等于b减2的互为相反数,则a的b平方等于多少 2020-05-16 …
(4)关于计算机技术指标的描述中,正确的是 A)奔腾芯片是 32位的,双核奔腾芯片是 64位的 B) 2020-05-23 …
(4)关于计算机技术指标的描述中,正确的是A)奔腾芯片是32位的,双核奔腾芯片是64位的B)平均浮点 2020-05-23 …
关于计算机技术指标的描述中,正确的是A.奔腾芯片是32位的,双核奔腾芯片是64位的B.平均浮点指令执 2020-05-23 …
关于椭圆方程的推导~关于推导x^2/a^2+y^2/b^=1时前一步,要令b^2=a^2-c^2. 2020-06-17 …
关于求根公式``很笨的问题,请不要见笑今天学了2次函数.里面有4ac-B平方我听同学说求跟公式里面 2020-06-26 …
1.按图中的程序计算,若开始输入的值为X=3,则最后输出的结果是输入X→→计算X(X+1)/2的值 2020-06-30 …
班加罗尔有“印度硅谷”之称,关于该工业区叙述正确的是()A.在当地丰富的能源资源基础上形成的B.平 2020-07-08 …