在数学课上，老师请同学思考如下问题：已知：在△ABC中，∠A=90°．求作：P，使得点P在AC上，且P与AB，BC都相切．小轩的作法如下：（1）作∠ABC的平分线BF，与AC交于点P；（2）以点P为

Question

在数学课上，老师请同学思考如下问题：
已知：在△ABC中，∠A=90°．
求作： P，使得点P在AC上，且 P与AB，BC都相切．
小轩的作法如下：

（1）作∠ABC的平分线BF，与AC交于点P；
（2）以点P为圆心，AP长为半径作 P． P即为所求．
老师说：“小轩的作法正确．”
请回答： P与BC相切的依据是___．

Answer 1

如图作PE⊥BC于E．

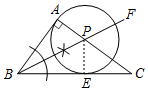
∵∠PBA=∠PBE，PA⊥AB，PE⊥BC，
∴PA=PE，
∴PE是 P的切线（角平分线上的点到角两边距离相等；经过半径的外端并且垂直于这条半径的直线是圆的切线．或：如果圆心到直线的距离等于半径，那么直线与圆相切）
故答案为角平分线上的点到角两边距离相等；经过半径的外端并且垂直于这条半径的直线是圆的切线（或：如果圆心到直线的距离等于半径，那么直线与圆相切）．