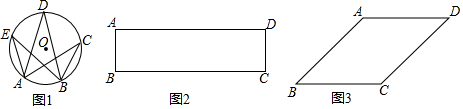
重温我们知道：同弧或等弧所对的圆周角相等．也就是，如图（1），⊙O中，AB所对的圆周角∠ACB=∠ADB=∠AEB．应用（1）已知：如图（2），矩形ABCD．①若AB<12BC，在边AD上求作点P，使∠BPC=90

Question

重温
我们知道：同弧或等弧所对的圆周角相等．也就是，如图（1），⊙O中，

AB

所对的圆周角∠ACB=∠ADB=∠AEB．

应用
（1）已知：如图（2），矩形ABCD．
①若AB<(1)/(2)BC，在边AD上求作点P，使∠BPC=90°．（保留作图痕迹，写出作法．）
②小明经研究发现，当AB、BC的大小关系发生变化时，①中点P的个数也会发生变化，请你就点P的个数，探讨AB与BC之间的数量关系．（直接写出结论）
创新
（2）小明经进一步研究发现：命题“若四边形的一组对边相等和一组对角相等，则这个四边形是平行四边形．”是一个假命题，并在平行四边形的基础上利用“同弧或等弧所对的圆周角相等．”作出了一个反例图形．请你利用下面如图（3）所给的□ABCD作出该反例图形．（不写作法，保留作图痕迹）

Answer 1

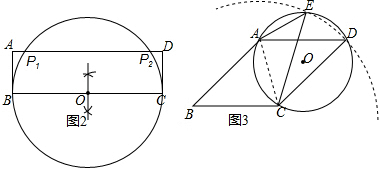（1）①如图2所示：
作法：以BC为直径作⊙O，交AD于P₁、P₂
P₁、P₂ 为所求作的点P，
②AB<(1)/(2)BC时，点P有两个；
AB=(1)/(2)BC时，点P有且只有1个；
AB>(1)/(2)BC时，点P有0个；

（2）如图3所示：
连接AC，作△ADC的外接圆⊙O，再以C为圆心，CD的长为半径画弧，与⊙O相交于点E，则四边形ABCE即为所求反例图形．